题目内容
(1)设函数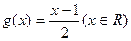 ,且数列
,且数列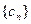 满足
满足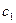 = 1,
= 1,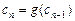 (n∈N,
(n∈N,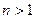 );求数列
);求数列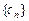 的通项公式.
的通项公式.
(2)设等差数列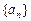 、
、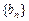 的前n项和分别为
的前n项和分别为 和
和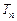 ,且
,且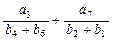
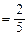 ,
,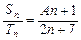 ,
, 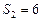 ;求常数A的值及
;求常数A的值及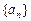 的通项公式.
的通项公式.
(3)若 ,其中
,其中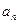 、
、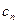 即为(1)、(2)中的数列
即为(1)、(2)中的数列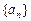 、
、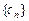 的第
的第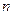 项,试求
项,试求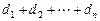
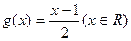 ,且数列
,且数列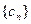 满足
满足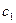 = 1,
= 1,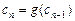 (n∈N,
(n∈N,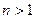 );求数列
);求数列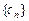 的通项公式.
的通项公式.(2)设等差数列
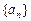 、
、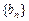 的前n项和分别为
的前n项和分别为 和
和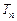 ,且
,且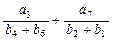
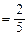 ,
,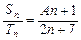 ,
, 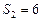 ;求常数A的值及
;求常数A的值及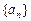 的通项公式.
的通项公式.(3)若
 ,其中
,其中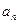 、
、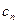 即为(1)、(2)中的数列
即为(1)、(2)中的数列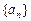 、
、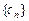 的第
的第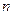 项,试求
项,试求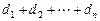
(1)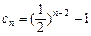 .(2)
.(2)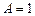 ;
;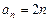 .
.
(3)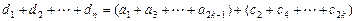
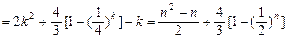
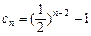 .(2)
.(2)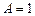 ;
;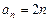 .
.(3)
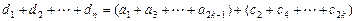
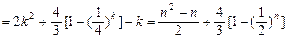
(1) 由题意: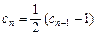 ,变形得:
,变形得: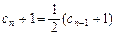 ,
,
∴数列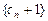 是以
是以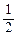 为公比,
为公比,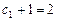 为首项的等比数列.
为首项的等比数列.
∴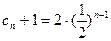 ,即
,即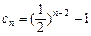 .
.
(2)∵由等差数列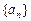 、
、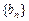 知:
知: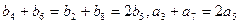 ;
;
∴由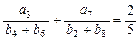 得:
得: ,
,
∴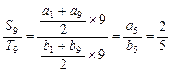 ,∵
,∵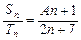 ,∴
,∴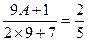 ,解得
,解得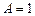 ;
;
∴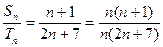 ,
, 和
和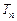 分别是等差数列
分别是等差数列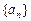 、
、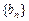 的前n项和;
的前n项和;
∴可设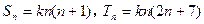 ; ∵
; ∵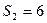 , ∴
, ∴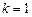 ,即
,即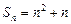 .
.
当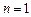 时,
时, ,
,
当n≥2时,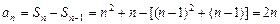 .
.
综上得: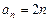 .
.
(3)当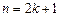 (
(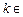 N*)时,
N*)时,
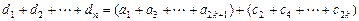
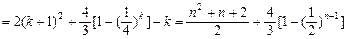
当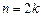 (
(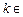 N*)时,
N*)时,
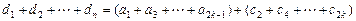
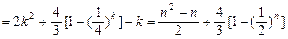
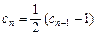 ,变形得:
,变形得: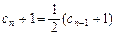 ,
, ∴数列
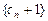 是以
是以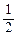 为公比,
为公比,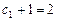 为首项的等比数列.
为首项的等比数列. ∴
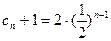 ,即
,即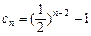 .
. (2)∵由等差数列
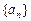 、
、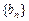 知:
知: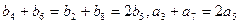 ;
;∴由
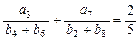 得:
得: ,
, ∴
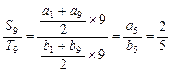 ,∵
,∵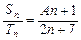 ,∴
,∴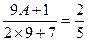 ,解得
,解得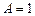 ;
;∴
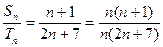 ,
, 和
和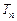 分别是等差数列
分别是等差数列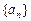 、
、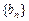 的前n项和;
的前n项和;∴可设
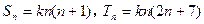 ; ∵
; ∵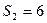 , ∴
, ∴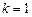 ,即
,即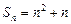 .
.当
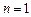 时,
时, ,
,当n≥2时,
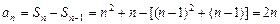 .
.综上得:
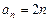 .
.(3)当
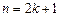 (
(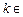 N*)时,
N*)时,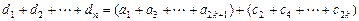
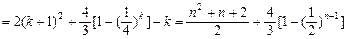
当
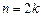 (
(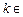 N*)时,
N*)时,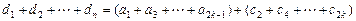
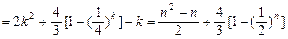

练习册系列答案
 明天教育课时特训系列答案
明天教育课时特训系列答案 浙江新课程三维目标测评课时特训系列答案
浙江新课程三维目标测评课时特训系列答案 周周清检测系列答案
周周清检测系列答案 轻巧夺冠周测月考直通高考系列答案
轻巧夺冠周测月考直通高考系列答案
相关题目
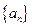 ,如果
,如果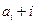 (
( =1,2,3,…)为完全平方数,则称数
=1,2,3,…)为完全平方数,则称数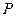 性质”。
性质”。 具有“
具有“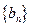 ,且
,且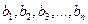 是
是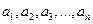 的一个排列
的一个排列 ;②数列
;②数列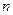 项和
项和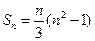 ,证明数列
,证明数列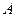 :1,2,3,…,
:1,2,3,…,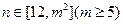 时,
时,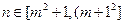 时,数
时,数 列
列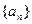 构成:
构成: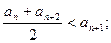
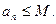 (n为正整数)
(n为正整数)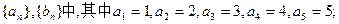
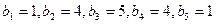 ;试判断数列
;试判断数列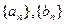 是否为集合W的元素;
是否为集合W的元素;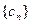 是各项为正的等比数列,
是各项为正的等比数列,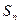 是其前n项和,
是其前n项和,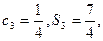 证明数列
证明数列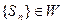 ;并写出M的取值范围;
;并写出M的取值范围;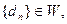 且对满足条件的M的最小值M0,都有
且对满足条件的M的最小值M0,都有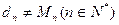 .
.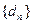 单调递增.
单调递增.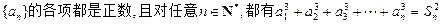 ,
,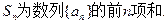
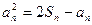 ;
;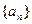 的通项公式;
的通项公式;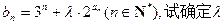 的取值范围,使得对任意
的取值范围,使得对任意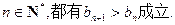
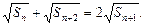
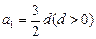 ,问是否存在正常数c,使
,问是否存在正常数c,使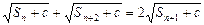 对任意自然数n都成立,若存在,求出c(用d表示);若不存在,说明理由.
对任意自然数n都成立,若存在,求出c(用d表示);若不存在,说明理由.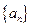 的前
的前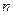 项和为
项和为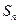 ,且对任意的
,且对任意的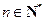 ,都有
,都有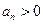 ,
,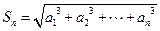 .
.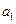 ,
,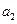 的值;
的值;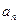 ;
;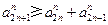 .
. 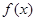 是定义在
是定义在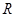 上恒不为零的函数,对任意的实数
上恒不为零的函数,对任意的实数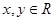 ,都有
,都有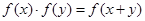 ,若
,若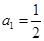 ,
,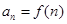 ,(
,(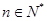 ),则数列
),则数列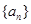 的前
的前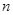 项和
项和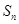 的最小值是( )
的最小值是( )
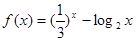 ,正实数
,正实数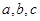 是公差为正数的等差数列,且满足
是公差为正数的等差数列,且满足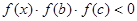 。若实数
。若实数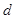 是方程
是方程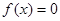 的一个解,那么下列四个判断:
的一个解,那么下列四个判断: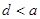 ;②
;②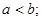 ③
③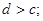 ④
④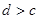 中有可能成立的个数为 ( )
中有可能成立的个数为 ( )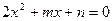 有实根,且2、
有实根,且2、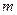 、
、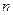 为等差数列的前三项.求该等差数列公差
为等差数列的前三项.求该等差数列公差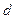 的取值范围.
的取值范围.