题目内容
现有两个命题:
(1)若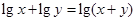 ,且不等式
,且不等式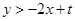 恒成立,则
恒成立,则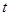 的取值范围是集合
的取值范围是集合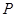 ;
;
(2)若函数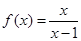 ,
,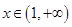 的图像与函数
的图像与函数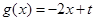 的图像没有交点,则
的图像没有交点,则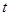 的取值范围是集合
的取值范围是集合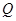 ;
;
则以下集合关系正确的是( )
(1)若
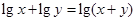 ,且不等式
,且不等式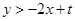 恒成立,则
恒成立,则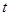 的取值范围是集合
的取值范围是集合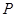 ;
;(2)若函数
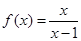 ,
,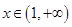 的图像与函数
的图像与函数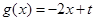 的图像没有交点,则
的图像没有交点,则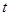 的取值范围是集合
的取值范围是集合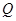 ;
;则以下集合关系正确的是( )
A.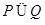 | B. | C.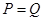 | D.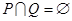 |
C
试题分析:法一、对(1):由
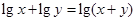 得
得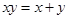 即
即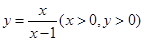 .
.不等式
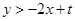 恒成立,等价于
恒成立,等价于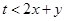 恒成立.这只需
恒成立.这只需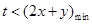 即可.
即可.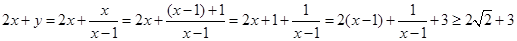 (当
(当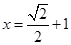 时,取等号).
时,取等号).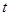 的取值范围是
的取值范围是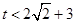 .
.对(2):作出函数
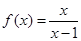 ,
,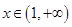 的图像与函数
的图像与函数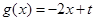 的图像如图所示:
的图像如图所示: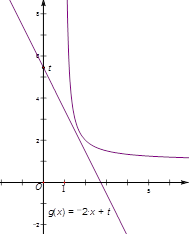
对
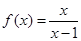 求导得:
求导得: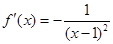 .由
.由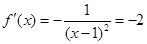 得
得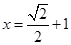 .由此得切点为
.由此得切点为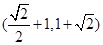 .代入
.代入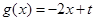 得
得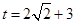 .由图可知
.由图可知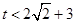 时,函数
时,函数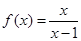 ,
,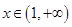 的图像与函数
的图像与函数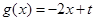 的图像没有交点,故
的图像没有交点,故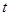 的取值范围为
的取值范围为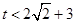 .
.综上得:
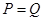 .所以选
.所以选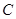 .
.法二、对(1):由
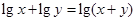 得
得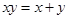 即
即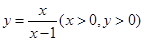 .
.由于
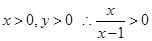 即
即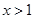 .
.由此可以看出,这两个问题,实质上是同一个问题.所以
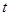 的取值范围相同.故选
的取值范围相同.故选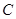 .
.
练习册系列答案
 期末好成绩系列答案
期末好成绩系列答案 99加1领先期末特训卷系列答案
99加1领先期末特训卷系列答案 百强名校期末冲刺100分系列答案
百强名校期末冲刺100分系列答案 好成绩1加1期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案
相关题目
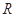 上的函数
上的函数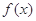 满足
满足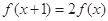 .若当
.若当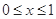 时.
时.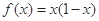 ,
,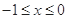 时,
时,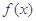 是定义在
是定义在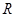 上的偶函数,且在
上的偶函数,且在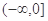 上是增函数,设
上是增函数,设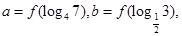
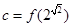 ,则
,则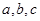 的大小关系是( )
的大小关系是( )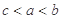
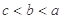
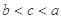
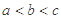
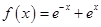 有最小值是
有最小值是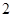 ;
;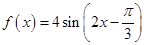 的图象关于点
的图象关于点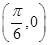 对称;
对称;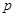 且
且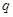 ”为假命题,则
”为假命题,则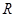 上的可导函数
上的可导函数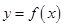 满足:对
满足:对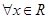 ,都有
,都有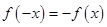 成立,
成立,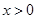 时,
时,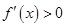 ,则当
,则当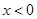 时,
时,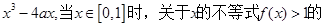 解集为空集,则满足条件的实数a的取值范围是 .
解集为空集,则满足条件的实数a的取值范围是 .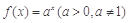 在[-1,2]上的最大值为4,最小值为m,且函数
在[-1,2]上的最大值为4,最小值为m,且函数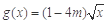 在
在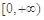 上是增函数,则a=( )
上是增函数,则a=( )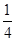
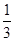
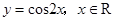
 且
且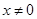
 ,
,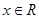
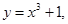
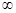 )上单调递减的是( )
)上单调递减的是( )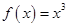
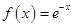
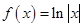
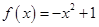
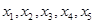 均不小于1,且
均不小于1,且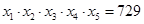 ,则
,则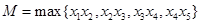 的最小值是 .(
的最小值是 .(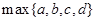 是指
是指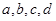 四个数中最大的一个)
四个数中最大的一个)