题目内容
给出下列四个命题:
①函数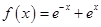 有最小值是
有最小值是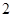 ;
;
②函数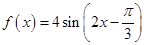 的图象关于点
的图象关于点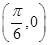 对称;
对称;
③若“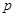 且
且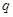 ”为假命题,则
”为假命题,则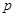 、
、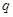 为假命题;
为假命题;
④已知定义在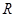 上的可导函数
上的可导函数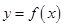 满足:对
满足:对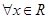 ,都有
,都有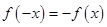 成立,
成立,
若当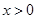 时,
时,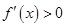 ,则当
,则当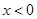 时,
时,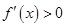 .
.
其中正确命题的序号是 .
①函数
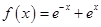 有最小值是
有最小值是 ;
;②函数
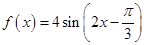 的图象关于点
的图象关于点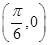 对称;
对称;③若“
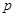 且
且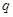 ”为假命题,则
”为假命题,则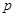 、
、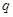 为假命题;
为假命题; ④已知定义在
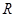 上的可导函数
上的可导函数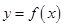 满足:对
满足:对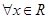 ,都有
,都有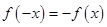 成立,
成立,若当
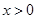 时,
时,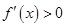 ,则当
,则当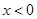 时,
时,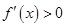 .
.其中正确命题的序号是 .
①②④.
试题分析:对于命题①,
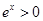 ,
,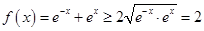 ,当且仅当
,当且仅当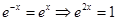 ,即当
,即当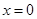 时,上式取等号,即函数
时,上式取等号,即函数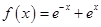 有最小值
有最小值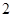 ,故命题①正确;对于命题②,由于
,故命题①正确;对于命题②,由于
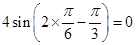 ,故函数
,故函数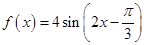 的图象关于点
的图象关于点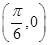 对称,故命题②正确;对于命题③,若“
对称,故命题②正确;对于命题③,若“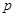 且
且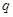 ”为假命题,则
”为假命题,则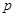 、
、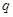 中至少有一个是假命题,故命题③错误;对于命题④,由于函数
中至少有一个是假命题,故命题③错误;对于命题④,由于函数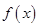 是奇函数,当
是奇函数,当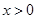 时,
时,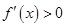 ,即函数
,即函数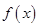 在区间
在区间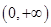 上单调递增,由奇函数的性质知,函数
上单调递增,由奇函数的性质知,函数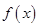 在
在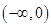 上也是单调递增的,即当
上也是单调递增的,即当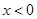 时,仍有
时,仍有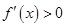 ,故命题④正确,综上所述,正确命题的序号是①②④.
,故命题④正确,综上所述,正确命题的序号是①②④.
练习册系列答案
相关题目
 ,
, 恒过定点 (3,2).
恒过定点 (3,2). ;
; 的图象向下平移1个单位,再向左平移
的图象向下平移1个单位,再向左平移 ,设函数
,设函数 ,求
,求 ,若在其定义域内,不等式
,若在其定义域内,不等式 恒成立,求
恒成立,求 的取值范围.
的取值范围.
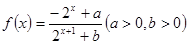 .
.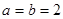 时,证明:函数
时,证明:函数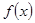 不是奇函数;
不是奇函数;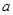 与
与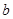 的值;
的值;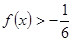 的解集.
的解集.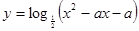 在区间
在区间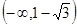 上为增函数,则
上为增函数,则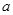 的取值范围是 __________.
的取值范围是 __________.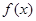 ,对任意
,对任意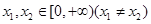 ,有
,有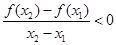 ,则 ( ).
,则 ( ).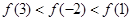
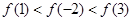
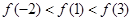
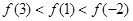
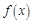 是偶函数,且当
是偶函数,且当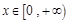 时,f (x) = x-1,则f (x-1) < 0的解集是( )
时,f (x) = x-1,则f (x-1) < 0的解集是( )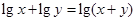 ,且不等式
,且不等式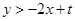 恒成立,则
恒成立,则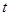 的取值范围是集合
的取值范围是集合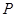 ;
;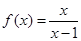 ,
,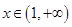 的图像与函数
的图像与函数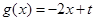 的图像没有交点,则
的图像没有交点,则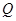 ;
;

 ,若对于任意的
,若对于任意的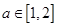 ,
,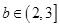 ,函数
,函数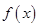 在区间
在区间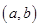 上单调递减,则实数
上单调递减,则实数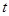 的取值范围是( )
的取值范围是( )