题目内容
【题目】已知函数![]() .
.
(1)当![]() 时,求曲线
时,求曲线![]() 在
在![]() 处的切线方程;
处的切线方程;
(2)讨论![]() 的单调性;
的单调性;
(3)设![]() 、
、![]() 为曲线
为曲线![]() 上的任意两点,并且
上的任意两点,并且![]() ,若
,若![]() 恒成立,证明:
恒成立,证明:![]() .
.
【答案】(1)![]() ;(2)若
;(2)若![]() ,
, ![]() 在
在![]() 上递增;若
上递增;若![]() ,
,![]() 时,
时,![]() 单调递增;
单调递增;![]() ,
,![]() 单调递减;(3)证明见解析.
单调递减;(3)证明见解析.
【解析】
(1)将![]() 代入可得函数解析式,求得导数并代入
代入可得函数解析式,求得导数并代入![]() 求得切线的斜率.将
求得切线的斜率.将![]() 代入函数可得切点坐标,由点斜式即可求得切线方程.
代入函数可得切点坐标,由点斜式即可求得切线方程.
(2)先求得导函数,对![]() 分类讨论,根据导函数的符号即可判断单调性.
分类讨论,根据导函数的符号即可判断单调性.
(3)根据![]() 恒成立及(2)中函数单调性的讨论,可求得
恒成立及(2)中函数单调性的讨论,可求得![]() .代入函数并结合不等式即可得
.代入函数并结合不等式即可得![]() .利用定义作差,得
.利用定义作差,得![]() ,化简后即可证明.
,化简后即可证明.
(1)当![]() 时,
时,![]() ,
,
对函数![]() 求导得
求导得![]() ,
,
∴![]() ,又
,又![]() ,
,
∴曲线![]() 在
在![]() 处的切线方程为:
处的切线方程为:![]() ;
;
(2)求导得![]() ,
,
若![]() ,
,![]() ,
,![]() 在
在![]() 上递增;
上递增;
若![]() ,当
,当![]() 时,
时,![]() ,
,![]() 单调递增;
单调递增;
当![]() 时,
时,![]() ,
,![]() 单调递减.
单调递减.
(3)由(2)知,若![]() ,
,![]() 在
在![]() 上递增,
上递增,
又![]() ,故
,故![]() 不恒成立.
不恒成立.
若![]() ,当
,当![]() 时,
时,![]() 递减,
递减,![]() ,不合题意.
,不合题意.
若![]() ,当
,当![]() 时,
时,![]() 递增,
递增,![]() ,不合题意.
,不合题意.
若![]() ,
,![]() 在
在![]() 上递增,在
上递增,在![]() 上递减,
上递减,![]() ,合题意.
,合题意.
故![]() ,且
,且![]() (当且仅当
(当且仅当![]() 时取“
时取“![]() ”).
”).
设![]() ,
,![]()
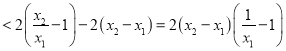 ,
,
∴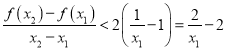 ,
,
因此,![]()
即![]()

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目