[题目]已知极点为直角坐标系的原点.极轴为轴正半轴且单位长度相同的极坐标系中曲线.(为参数).(Ⅰ)求曲线上的点到曲线距离的最小值,(Ⅱ)若把上各点的横坐标都扩大原来为原来的2倍.纵坐标扩大原来的倍.得到曲线.设.曲线与交于.两点.求. 题目和参考答案——青夏教育精英家教网—

题目内容

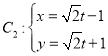【题目】已知极点为直角坐标系的原点，极轴为轴正半轴且单位长度相同的极坐标系中曲线，（为参数）.

（Ⅰ）求曲线上的点到曲线距离的最小值；

（Ⅱ）若把上各点的横坐标都扩大原来为原来的2倍，纵坐标扩大原来的倍，得到曲线，设，曲线与交于，两点，求.

【答案】（Ⅰ）；（Ⅱ）

【解析】

（Ⅰ）求出曲线C1的直角坐标方程为：x2+y2＝1，C2：y＝x+2，再求出圆心到直线距离，由此能求出曲线C1上的点到曲线C2距离的最小值；

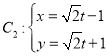（Ⅱ）利用伸缩变换得到，把（为参数）化成标准方程为：, 代入曲线，得．由此能求出|PA|+|PB|．

（Ⅰ），圆心为，半径为，

圆心到直线距离，所以上的点到的最小距离为；

（Ⅱ）伸缩变换为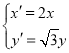，所以

把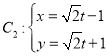（为参数）化成标准方程为：,

将和联立，得.因为

练习册系列答案

（1）如果从第8行第7列的数开始向右读，请你依次写出最先检查的3个人的编号；

（下面摘取了第7行到第9行）

84 42 17 53 31 57 24 55 06 88 77 04 74 47 67 21 76 33 50 25 83 92 12 06 76

63 01 63 78 59 16 95 56 67 19 98 10 50 71 75 12 86 73 58 07 44 39 52 38 79

33 21 12 34 29 78 64 56 07 82 52 42 07 44 38 15 51 00 13 42 99 66 02 79 54

（2）抽取的100人的数学与地理的水平测试成绩如下表：

成绩分为优秀、良好、及格三个等级；横向，纵向分别表示地理成绩与数学成绩，例如：表中数学成绩为良好的共有20+18+4=42．

人数		数学
人数		优秀	良好	及格
地理	优秀	7	20	5
	良好	9	18	6
	及格	a	4	b

①若在该样本中，数学成绩优秀率是30％，求a,b的值：

②在地理成绩及格的学生中，已知求数学成绩优秀的人数比及格的人数少的概率．

【题目】定义,已知函数、定义域都是，给出下列命题：

（1）若、都是奇函数,则函数为奇函数；

（2）若、都是减函数,则函数为减函数；

（3）若,,则；

（4）若、都是周期函数,则函数是周期函数.

其中正确命题的个数为（）

A.1个B.2个C.3个D.4个

【题目】如图1,某小区中有条长为50米,宽为6.5米的道路ABCD,在路的一侧可以停放汽车,已知小型汽车的停车位是一个2.5米宽,5米长的矩形,如GHPQ,这样该段道路可以划岀10个车位,随着小区居民汽车拥有量的增加,停车难成为普遍现象.经过各方协商,小区物业拟压缩绿化,拓宽道路,改变车位方向增加停车位,如图2,改建后的通行宽度保持不变,即G到AD的距离不变.

(1)绿化被压缩的宽度BE与停车位的角度∠HPE有关,记为停车方便,要求,写出关于的函数表达式；

(2)沿用(1)的条件和记号,实际施工时,BE=3米,问改造后的停车位增加了多少个?

【题目】为了解户籍、性别对生育二胎选择倾向的影响，某地从育龄人群中随机抽取了容量为200的调查样本，其中城镇户籍与农村户籍各100人；男性120人，女性80人，绘制不同群体中倾向选择生育二胎与倾向选择不生育二胎的人数比例图，如图所示，其中阴影部分表示倾向选择生育二胎的对应比例，则下列叙述中错误的是( )

A. 是否倾向选择生育二胎与户籍有关

B. 是否倾向选择生育二胎与性别有关

C. 倾向选择生育二胎的人群中，男性人数与女性人数相同

D. 倾向选择不生育二胎的人群中，农村户籍人数少于城镇户籍人数

【题目】已知函数.

（1）当时，求曲线在处的切线方程；

（2）讨论的单调性；

（3）设、为曲线上的任意两点，并且，若恒成立，证明：.

【题目】已知四边形ABCD为边长等于的正方形，PA⊥平面ABCD，QC∥PA，且异面直线QD与PA所成的角为30°，则四棱锥Q－ABCD外接球的表面积等于( )

A. B. C. D.

【题目】党的十九大明确把精准脱贫作为决胜全面建成小康社会必须打好的三大攻坚战之一，为坚决打赢脱贫攻坚战，某帮扶单位为帮助定点扶贫村扶贫，此帮扶单位为了解该村贫困户对其所提供帮扶的满意度，随机调查了40个贫困户，得到贫困户的满意度评分如下：

贫困户编号	评分	贫困户编号	评分	贫困户编号	评分	贫困户编号	评分
1	78	11	88	21	79	31	93
2	73	12	86	22	83	32	78
3	81	13	95	23	72	33	75
4	92	14	76	24	74	34	81
5	86	15	80	25	93	35	89
6	85	16	78	26	66	36	77
7	79	17	88	27	80	37	81
8	84	18	82	28	83	38	76
9	63	19	76	29	74	39	85
10	85	20	87	30	82	40	78

用系统抽样法从40名贫困户中抽取容量为8的样本，且在第一分段里随机抽到的评分数据为86．

（1）请你列出抽到的8个样本的评分数据；

（2）计算所抽到的8个样本的均值和方差；

（3）在（2）条件下，若贫困户的满意度评分在之间，则满意度等级为“A级”．运用样本估计总体的思想，现从（1）中抽到的8个样本的满意度为“A级”贫困户中随机地抽取2户，求所抽到2户的满意度评分均“超过85”的概率．（参考数据：，，）

【题目】设双曲线的左右焦点分别为，过的直线分别交双曲线左右两支于点M，N.若以MN为直径的圆经过点且，则双曲线的离心率为（）

A.B.C.D.

试题分类