题目内容
【题目】设计一个随机试验,使一个事件的概率与某个未知数有关,然后通过重复试验,以频率估计概率,即可求得未知数的近似解,这种随机试验在数学上称为随机模拟法,也称为蒙特卡洛法。比如要计算一个正方形内部不规则图形的面积,就可以利用撒豆子,计算出落在不规则图形内部和正方形内部的豆子数比近似等于不规则图形面积与正方形面积比,从而近似求出不规则图形的面积.
统计学上还有一个非常著名的蒲丰投针实验:平面上间隔![]() 的平行线,向平行线间的平面上任意投掷一枚长为
的平行线,向平行线间的平面上任意投掷一枚长为![]() 的针
的针![]() ,通过多次实验可以近似求出针与任一平行线(以
,通过多次实验可以近似求出针与任一平行线(以![]() 为例)相交(当针的中点在平行线外不算相交)的概率.以
为例)相交(当针的中点在平行线外不算相交)的概率.以![]() 表示针的中点与最近一条平行线
表示针的中点与最近一条平行线![]() 的距离,又以
的距离,又以![]() 表示
表示![]() 与
与![]() 所成夹角,如图甲,易知满足条件:
所成夹角,如图甲,易知满足条件:![]() ,
,![]() .
.
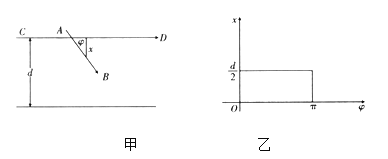
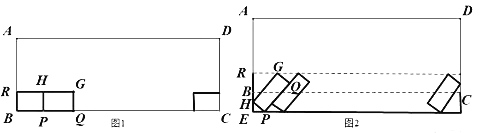
由这两式可以确定平面上的一个矩形![]() ,如图乙,在图甲中,当
,如图乙,在图甲中,当![]() 满足___________(
满足___________(![]() 与
与![]() ,
,![]() 之间的关系)时,针与平行线相交(记为事件
之间的关系)时,针与平行线相交(记为事件![]() ).可用从实验中获得的频率去近似
).可用从实验中获得的频率去近似![]() ,即投针
,即投针![]() 次,其中相交的次数为
次,其中相交的次数为![]() ,则
,则![]() ,历史上有一个数学家亲自做了这实验,他投掷的次数是5000,相交的次数为2550次,
,历史上有一个数学家亲自做了这实验,他投掷的次数是5000,相交的次数为2550次,![]() ,
,![]() ,依据这个实验求圆周率
,依据这个实验求圆周率![]() 的近似值_________.(精确到3位小数)
的近似值_________.(精确到3位小数)
【答案】![]()
![]()
【解析】
根据几何性质可得![]() ,利用定积分求出由
,利用定积分求出由![]() 轴、曲线
轴、曲线![]() 围成的面积后可得
围成的面积后可得![]() 的值,结合频率可求
的值,结合频率可求![]() 的近似值.
的近似值.
由图知![]() ,将已知数据代入可得:
,将已知数据代入可得: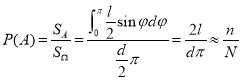 ,
,![]() .
.
故答案为: ![]()
![]() .
.

练习册系列答案
相关题目