题目内容
【题目】数列![]() 满足:对一切
满足:对一切![]() ,有
,有![]() ,其中
,其中![]() 是与
是与![]() 无关的常数,称数列上有界(有上界),并称
无关的常数,称数列上有界(有上界),并称![]() 是它的一个上界,对一切
是它的一个上界,对一切![]() ,有
,有![]() ,其中
,其中![]() 是与
是与![]() 无关的常数,称数列下有界(有下界),并称
无关的常数,称数列下有界(有下界),并称![]() 是它的一个下界.一个数列既有上界又有下界,则称为有界数列,常值数列是一个特殊的有界数列.设
是它的一个下界.一个数列既有上界又有下界,则称为有界数列,常值数列是一个特殊的有界数列.设![]() ,数列
,数列![]() 满足
满足![]() ,
,![]() ,
,![]() .
.
(1)若数列![]() 为常数列,试求实数
为常数列,试求实数![]() 、
、![]() 满足的等式关系,并求出实数
满足的等式关系,并求出实数![]() 的取值范围;
的取值范围;
(2)下面四个选项,对一切实数![]() ,恒正确的是.(写出所有正确选项,不需要证明其正确,但需要简单说明一下为什么不选余下几个)
,恒正确的是.(写出所有正确选项,不需要证明其正确,但需要简单说明一下为什么不选余下几个)
A. 当![]() 时,
时,![]() B. 当
B. 当![]() 时,
时,![]()
C. 当![]() 时,
时,![]() D. 当
D. 当![]() 时,
时,![]()
(3)若![]() ,
,![]() ,且数列
,且数列![]() 是有界数列,求
是有界数列,求![]() 的值及
的值及![]() 的取值范围.
的取值范围.
【答案】(1)![]() ,
,![]() ;(2)B;(3)
;(2)B;(3)![]() ,
,![]() .
.
【解析】
(1)利用![]() 列方程,根据方程有实数根,求得
列方程,根据方程有实数根,求得![]() 的取值范围.
的取值范围.
(2)利用(1)的结论,判断出错误选项,由此得出正确选项.
(3)对![]() 分成
分成![]() 两种情况进行分类讨论,根据
两种情况进行分类讨论,根据![]() 的上界和下界,列不等式,由此求得
的上界和下界,列不等式,由此求得![]() 的值和
的值和![]() 的取值范围.
的取值范围.
(1)由于数列![]() 为常数列,所以
为常数列,所以![]() ,故
,故![]() ,即
,即![]() ,此方程有实数根,故
,此方程有实数根,故![]() ,解得
,解得![]() ,即实数
,即实数![]() 的取值范围是
的取值范围是![]() .
.
(2)由(1)可知,当数列![]() 为常数列时,实数
为常数列时,实数![]() 的取值范围是
的取值范围是![]() ,此时
,此时![]() 的值与
的值与![]() 有关,不一定大于
有关,不一定大于![]() ,故ACD三个选项不正确,B选项正确.
,故ACD三个选项不正确,B选项正确.
(3) 依题意,大前提为:![]() ,
,![]()
①当![]() 为常数列时,由(1)知
为常数列时,由(1)知![]() ,所以
,所以![]() ,
,![]() ,
,![]() .
.
②当![]() 不是常数列时,由于
不是常数列时,由于![]() ,
,![]() ,故数列
,故数列![]() 是单调递增数列.最小值为
是单调递增数列.最小值为![]() ,设对一切
,设对一切![]() ,有
,有![]() ,故
,故![]() (
(![]() ).
).
i)当![]() 时,
时,![]() ,所以
,所以![]() ,即
,即![]() ,故
,故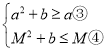 ,由于
,由于![]() 成立,故③成立.由④得
成立,故③成立.由④得![]() ,即存在实数
,即存在实数![]() 使上式成立,故
使上式成立,故![]() ,而本题大前提是
,而本题大前提是![]() ,所以
,所以![]() .此时
.此时![]() ,所以
,所以![]() .所以
.所以![]() ,即
,即![]() .
.
ii)当![]() 时,
时,![]() ,故
,故![]() .
.
若![]() ,则
,则![]() ,
,![]() ,即
,即![]() ,则
,则![]() ,
,![]() ,其判别式
,其判别式![]() ,故不存在
,故不存在![]() 使
使![]() 成立.
成立.
所以![]() ,此时
,此时![]() ,
,![]() ,即
,即![]() ,故
,故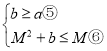 ,⑤恒成立.对于⑥,由④的分析可知,
,⑤恒成立.对于⑥,由④的分析可知,![]() ,
,![]() .所以
.所以![]() ,解得
,解得![]() .
.
综上所述,![]() ,
,![]() .
.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目