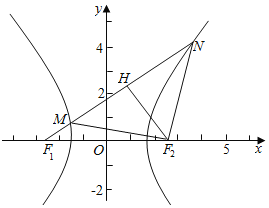
[题目]设双曲线的左右焦点分别为.过的直线分别交双曲线左右两支于点M.N.若以MN为直径的圆经过点且.则双曲线的离心率为( )A.B.C.D. 题目和参考答案——青夏教育精英家教网—

题目内容

【题目】设双曲线的左右焦点分别为，过的直线分别交双曲线左右两支于点M，N.若以MN为直径的圆经过点且，则双曲线的离心率为（）

A.B.C.D.

【答案】C

【解析】

由题意可得△MNF2为等腰直角三角形，设|MF2|＝|NF2|＝m，则|MN|m，运用双曲线的定义，求得|MN|＝4a，可得m，再由勾股定理可得a，c的关系，即可得到所求离心率．

若以MN为直径的圆经过右焦点F2，

则，又|MF2|＝|NF2|，

可得△MNF2为等腰直角三角形，

设|MF2|＝|NF2|＝m，则|MN|m，

由|MF2|﹣|MF1|＝2a，|NF1|﹣|NF2|＝2a，

两式相加可得|NF1|﹣|MF1|＝|MN|＝4a，

即有m＝2a，

在直角三角形HF1F2中可得

4c2＝4a2+（2a+2a﹣2a）2，

化为c2＝3a2，

即e．

故选C．

练习册系列答案

相关题目

【题目】在直角坐标系中，以原点为极点，轴的正半轴为极轴，以相同的长度单位建立极坐标系，已知直线的极坐标方程为，曲线的极坐标方程为，

（l）设为参数，若，求直线的参数方程；

（2）已知直线与曲线交于，设，且，求实数的值.

【题目】如图1,某小区中有条长为50米,宽为6.5米的道路ABCD,在路的一侧可以停放汽车,已知小型汽车的停车位是一个2.5米宽,5米长的矩形,如GHPQ,这样该段道路可以划岀10个车位,随着小区居民汽车拥有量的增加,停车难成为普遍现象.经过各方协商,小区物业拟压缩绿化,拓宽道路,改变车位方向增加停车位,如图2,改建后的通行宽度保持不变,即G到AD的距离不变.

(1)绿化被压缩的宽度BE与停车位的角度∠HPE有关,记为停车方便,要求,写出关于的函数表达式；

(2)沿用(1)的条件和记号,实际施工时,BE=3米,问改造后的停车位增加了多少个?

【题目】已知函数.

（1）当时，求曲线在处的切线方程；

（2）讨论的单调性；

（3）设、为曲线上的任意两点，并且，若恒成立，证明：.

【题目】已知四边形ABCD为边长等于的正方形，PA⊥平面ABCD，QC∥PA，且异面直线QD与PA所成的角为30°，则四棱锥Q－ABCD外接球的表面积等于( )

A. B. C. D.

【题目】设函数，

(1) 若，求函数的单调区间；

(2) 若函数有两个零点，求实数a的取值范围.

【题目】党的十九大明确把精准脱贫作为决胜全面建成小康社会必须打好的三大攻坚战之一，为坚决打赢脱贫攻坚战，某帮扶单位为帮助定点扶贫村扶贫，此帮扶单位为了解该村贫困户对其所提供帮扶的满意度，随机调查了40个贫困户，得到贫困户的满意度评分如下：

贫困户编号	评分	贫困户编号	评分	贫困户编号	评分	贫困户编号	评分
1	78	11	88	21	79	31	93
2	73	12	86	22	83	32	78
3	81	13	95	23	72	33	75
4	92	14	76	24	74	34	81
5	86	15	80	25	93	35	89
6	85	16	78	26	66	36	77
7	79	17	88	27	80	37	81
8	84	18	82	28	83	38	76
9	63	19	76	29	74	39	85
10	85	20	87	30	82	40	78

用系统抽样法从40名贫困户中抽取容量为8的样本，且在第一分段里随机抽到的评分数据为86．

（1）请你列出抽到的8个样本的评分数据；

（2）计算所抽到的8个样本的均值和方差；

（3）在（2）条件下，若贫困户的满意度评分在之间，则满意度等级为“A级”．运用样本估计总体的思想，现从（1）中抽到的8个样本的满意度为“A级”贫困户中随机地抽取2户，求所抽到2户的满意度评分均“超过85”的概率．（参考数据：，，）

【题目】已知数列满足，，.

（1）若，写出所有可能的值；

（2）若数列是递增数列，且、、成等差数列，求p的值；

（3）若，且是递增数列，是递减数列，求数列的通项公式.

【题目】某学校为了解学生假期参与志愿服务活动的情况，随机调查了名男生，名女生，得到他们一周参与志愿服务活动时间的统计数据如右表（单位：人）：

	超过小时	不超过小时
男
女

（1）能否有的把握认为该校学生一周参与志愿服务活动时间是否超过小时与性别有关？

（2）以这名学生参与志愿服务活动时间超过小时的频率作为该事件发生的概率，现从该校学生中随机抽查名学生，试估计这名学生中一周参与志愿服务活动时间超过小时的人数.

附：

试题分类