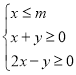题目内容
【题目】已知数列
的前
项和
满足，
.数列
的前项和为
，则满足
的最小的值为______．
【答案】7
【解析】
根据题意，将Sn＝3an﹣2变形可得Sn﹣1＝3an﹣1﹣2，两式相减变形，并令n＝1求出a1的值，即可得数列{an}是等比数列，求得数列{an}的通项公式，再由错位相减法求出Tn的值，利用Tn＞100，验证分析可得n的最小值，即可得答案．
根据题意，数列{an}满足Sn＝3an﹣2，①
当n≥2时，有Sn﹣1＝3an﹣1﹣2，②，
①﹣②可得：an＝3an﹣3an﹣1，变形可得2an＝3an﹣1，
当n＝1时，有S1＝a1＝3a1﹣2，解可得a1＝1，
则数列{an}是以a1＝1为首项，公比为
的等比数列，则an＝（）n﹣1，
数列{nan}的前n项和为Tn，则Tn＝1+2
3×（）2+……+n×（）n﹣1，③
则有Tn
2×（）2+3×（）3+……+n×（）n，④
③﹣④可得：
Tn＝1+（）+（）2+……×（）n﹣1﹣n×（）n＝﹣2（1
）﹣n×（）n，
变形可得：Tn＝4+（2n﹣4）×（）n，
若Tn＞100，即4+（2n﹣4）×（）n＞100，
分析可得：n≥7，故满足Tn＞100的最小的n值为7；
故答案为：7．
【题目】某水果种植基地引进一种新水果品种，经研究发现该水果每株的产量
（单位：
）和与它“相近”的株数
具有线性相关关系（两株作物“相近”是指它们的直线距离不超过
），并分别记录了相近株数为0，1，2，3，4时每株产量的相关数据如下：
| 0 | 1 | 2 | 3 | 4 |
| 15 | 12 | 11 | 9 | 8 |
（1）求出该种水果每株的产量关于它“相近”株数的回归方程；
（2）有一种植户准备种植该种水果500株，且每株与它“相近”的株数都为
，计划收获后能全部售出，价格为10元
，如果收入（收入=产量×价格）不低于25000元，则
的最大值是多少？
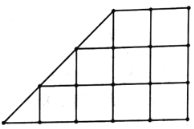
（3）该种植基地在如图所示的直角梯形地块的每个交叉点（直线的交点）处都种了一株该种水果，其中每个小正方形的边长和直角三角形的直角边长都为，已知该梯形地块周边无其他树木影响，若从所种的该水果中随机选取一株，试根据（1）中的回归方程，预测它的产量的分布列与数学期望.
附：回归方程
中斜率和截距的最小二乘法估计公式分别为：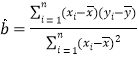
，
.
