Question

【题目】已知椭圆C：的左、右顶点分别为A，B，离心率为，点P（1，）为椭圆上一点．

（1）求椭圆C的标准方程；

（2）如图，过点C（0，1）且斜率大于1的直线l与椭圆交于M，N两点，记直线AM的斜率为k1，直线BN的斜率为k2，若k1=2k2，求直线l斜率的值．

Answer 1

【答案】(1);(2)

【解析】

（1）根据题意，由椭圆离心率可得a=2c，进而可得，则椭圆的标准方程为，将P的坐标代入计算可得c的值，即可得答案；

（2）根据题意，设直线l的方程为y=kx+1，设M（x1，y1），N（x2，y2），将直线的方程与椭圆联立，可得（3+4k2）x2+8kx-8=0，由根与系数的关系分析，：，，结合椭圆的方程与直线的斜率公式可得，即12k2-20k+3=0，解可得k的值，即可得答案．

解：（1）根据题意，椭圆的离心率为，即e==2，则a=2c．

又∵a2=b2+c2，∴．

∴椭圆的标准方程为：．

又∵点P（1，）为椭圆上一点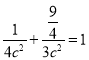，∴，解得：c=1．

∴椭圆的标准方程为：．

（2）由椭圆的对称性可知直线l的斜率一定存在，设其方程为y=kx+1．

设M（x1，y1），N（x2，y2）．

联列方程组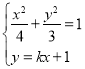：，消去y可得：（3+4k2）x2+8kx-8=0．

∴由韦达定理可知：，．

∵，，且k1=2k2，∴，即．①

又∵M（x1，y1），N（x2，y2）在椭圆上，

∴，．②

将②代入①可得：，即3x1x2+10（x1+x2）+12=0．

∴，即12k2-20k+3=0．

解得：或．

又由k＞1，则．