题目内容
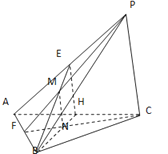
【题目】如图，在三棱锥
中，
是边长为2的正三角形，
，E、F、H分别为AP、AB、AC的中点，PF交BE于点M，CF交BH于点N，
，
．
求证：
平面BEH；
求证：
；
求直线PA与平面ABC所成角的正弦值．
【答案】（1）证明见解析；（2）证明见解析；（3）
。
【解析】
（1）推导出BH⊥AC，EH⊥AC，由此能证明AC⊥平面BEH．
（2）推导出N是△ABC的重心，M是△ABP的重心，从而
，由此能证明PC∥MN．
（3）取BH的中点G，连结AG，推导出EG⊥BH，EG⊥AC，EG⊥平面ABC，从而∠EAG是PA与平面ABC所成角，由此能求出直线PA与平面ABC所成角的正弦值．
证明：
是边长为2的正三角形，H是AC中点，
，
，E、H分别为AP、AC的中点，
，
，
，
平面BEH．
证明：
交BE于点M，CF交BH于点N，
是边长为2的正三角形，
，E、F、H分别为AP、AB、AC的中点，
是的重心，
，M是
的重心，
，
，
．
取BH的中点G，连结AG，
，
，
平面BEH，
，
平面ABC，
是PA与平面ABC所成角，
在
中，
，
，
，
直线PA与平面ABC所成角的正弦值为．
练习册系列答案
相关题目
