题目内容
14.对于原命题“正弦函数不是分段函数”,陈述正确的是( )| A. | 否命题是“正弦函数是分段函数 | |
| B. | 逆否命题是“分段函数不是正弦函数” | |
| C. | 逆否命题是“分段函数是正弦函数” | |
| D. | 以上都不正确 |
分析 把原命题变成若p,则q的形式:“若一个函数是正弦函数,则它不是分段函数”,这样便容易写出它的否命题,及其逆否命题,从而找出正确选项.
解答 解:否命题为:“不是正弦函数,便是分段函数”,∴A错误;
逆否命题为:“若一个函数是分段函数,则它不是正弦函数”,也可说成“分段函数不是正弦函数”,∴B正确.
故选B.
点评 考查分段函数的形式,正弦函数的表示形式:y=sinx,以及原命题、逆否命题的表达形式.

练习册系列答案
相关题目
5.奇函数f(x)满足f(x+2)=-f(x),当x∈(0,1)时,f(x)=3x+$\frac{1}{2}$,则f(log354)=( )
| A. | -2 | B. | -$\frac{7}{6}$ | C. | $\frac{7}{6}$ | D. | 2 |
2.已知复数$\frac{a+i}{1-i}$在复平面内对应的点在虚轴上(不含原点),则实数a=( )
| A. | -1 | B. | 1 | C. | $\frac{1}{2}$ | D. | $-\frac{1}{2}$ |
6.若$θ=[\frac{π}{4},\frac{π}{2}]$,sin2θ=$\frac{4}{5}$,则tanθ=( )
| A. | $\frac{4}{3}$ | B. | $\frac{3}{4}$ | C. | 2 | D. | $\frac{1}{2}$ |
3.已知a>b>0,则$\sqrt{a}$-$\sqrt{b}$与$\sqrt{a-b}$的大小关系是( )
| A. | $\sqrt{a}$-$\sqrt{b}$>$\sqrt{a-b}$ | B. | $\sqrt{a}$-$\sqrt{b}$<$\sqrt{a-b}$ | C. | $\sqrt{a}$-$\sqrt{b}$=$\sqrt{a-b}$ | D. | 无法确定 |
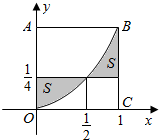 在如图的正方形OABC内任取一点,此点在由曲线y=x2和直线x=0,x=1,y=$\frac{1}{4}$所围成的阴影部分中的概率为$\frac{1}{4}$.
在如图的正方形OABC内任取一点,此点在由曲线y=x2和直线x=0,x=1,y=$\frac{1}{4}$所围成的阴影部分中的概率为$\frac{1}{4}$.