题目内容
9.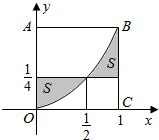 在如图的正方形OABC内任取一点,此点在由曲线y=x2和直线x=0,x=1,y=$\frac{1}{4}$所围成的阴影部分中的概率为$\frac{1}{4}$.
在如图的正方形OABC内任取一点,此点在由曲线y=x2和直线x=0,x=1,y=$\frac{1}{4}$所围成的阴影部分中的概率为$\frac{1}{4}$.
分析 首先利用定积分求出阴影部分的面积,然后利用几何概型公式解答.
解答 解:由曲线y=x2和直线x=0,x=1,y=$\frac{1}{4}$所围成的阴影部分面积为${∫}_{0}^{\frac{1}{2}}(\frac{1}{4}-{x}^{2})dx+{∫}_{\frac{1}{2}}^{1}({x}^{2}-\frac{1}{4})dx$=($\frac{1}{4}x-\frac{1}{3}{x}^{3}){|}_{0}^{\frac{1}{2}}$|${\;}_{0}^{\frac{1}{2}}$+($\frac{1}{3}{x}^{3}-\frac{1}{4}x$)|${\;}_{\frac{1}{2}}^{1}$=$\frac{1}{4}$,
正方形的面积为1,由几何概型的公式得到所求概率为$\frac{1}{4}$;
故答案为:$\frac{1}{4}$.
点评 本题考查了几何概型的概率求法以及利用定积分求曲边梯形的面积;关键是正确求出阴影部分的面积.

练习册系列答案
相关题目
20.已知a∈R,复数z=$\frac{n-i}{1-i}$是纯虚数(i是虚数单位),则a=( )
| A. | -$\sqrt{2}$ | B. | -1 | C. | 1 | D. | $\sqrt{2}$ |
4.小吴同学计划大学毕业后出国留学,其父母于2014年7月1日在银行存入a元钱,此后每年7月1日存入a元钱,若年利润为p且保持不变,并约定每年到期,存款的本息均自动转为新的一年的定期,在小吴同学2019年7月1日大学毕业时取出这五笔存款,则可以取出的钱(元)的总数为( )
| A. | a(1+p)5 | B. | a(1+p)6 | C. | $\frac{a}{p}$[(1+p)5-(1+p)] | D. | $\frac{a}{p}$[(1+p)6-(1+p)] |
14.对于原命题“正弦函数不是分段函数”,陈述正确的是( )
| A. | 否命题是“正弦函数是分段函数 | |
| B. | 逆否命题是“分段函数不是正弦函数” | |
| C. | 逆否命题是“分段函数是正弦函数” | |
| D. | 以上都不正确 |
1.已知a∈R,复数z=$\frac{a-i}{1-i}$是纯虚数(i数虚数单位),则a=( )
| A. | $-\sqrt{2}$ | B. | -1 | C. | 1 | D. | $\sqrt{2}$ |
19.已知全集U={-2,-1,0,1,2,3},A={-1,0,1,2},∁UB={-1,0,3},则A∩B=( )
| A. | {0,1,2} | B. | {1,3} | C. | {-2,1,2} | D. | {1,2} |