题目内容
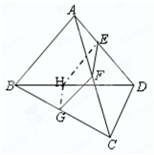
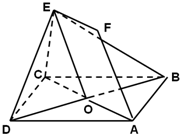
如图,正方形ABCD和四边形ACEF所在的平面互相垂直.EF∥AC,AB=
,CE=EF=1,∠ECA=60°.
(1)求证:AF∥平面BDE;
(2)求异面直线AB与DE所成角的余弦值.
| 2 |
(1)求证:AF∥平面BDE;
(2)求异面直线AB与DE所成角的余弦值.

(1)证明:∵ABCD是正方形,且AB=
,
∴AO=1,又EF∥AC,EF=1,
∴EFAO为平行四边形,则AF∥OE,而AF?面BDE,OE?面BDE,
∴AF∥面BDE(3分)
(2)∵ABCD是正方形,
∴AB∥CD
∴∠EDC为异面直线AB与DE所成的角或其补角(2分)
又BD⊥AC,又面ABCD⊥面ACEF,且面ABCD∩面ACEF=AC
∴BD⊥面ACEF,又OE?面ACEF,
∴BD⊥OE.
而由EC=1,OC=OA=1,∠ECA=60°
∴OE=1,又OD=1,则ED=
=
又CD=
,CE=1,
∴Cos∠EDC=
=
∴异面直线AB与DE所成的角的余弦值为
(3分)
| 2 |
∴AO=1,又EF∥AC,EF=1,
∴EFAO为平行四边形,则AF∥OE,而AF?面BDE,OE?面BDE,
∴AF∥面BDE(3分)
(2)∵ABCD是正方形,
∴AB∥CD
∴∠EDC为异面直线AB与DE所成的角或其补角(2分)
又BD⊥AC,又面ABCD⊥面ACEF,且面ABCD∩面ACEF=AC
∴BD⊥面ACEF,又OE?面ACEF,
∴BD⊥OE.
而由EC=1,OC=OA=1,∠ECA=60°
∴OE=1,又OD=1,则ED=
| OE2+OD2 |
| 2 |
又CD=
| 2 |
∴Cos∠EDC=
| 2+2-1 | ||||
2×
|
| 3 |
| 4 |
∴异面直线AB与DE所成的角的余弦值为
| 3 |
| 4 |

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目