题目内容
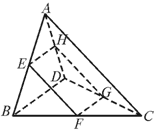
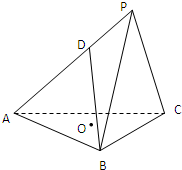
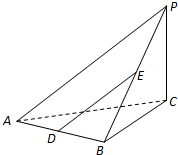
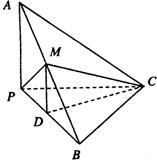
如图，在三棱锥A-BPC中，AP⊥PC，AC⊥BC，M为AB中点，D为PB中点，且△PMB为正三角形，
（Ⅰ）求证：MD∥平面APC；
（Ⅱ）求证：平面ABC⊥平面APC．
（Ⅰ）求证：MD∥平面APC；
（Ⅱ）求证：平面ABC⊥平面APC．
证明：（Ⅰ）∵M为AB中点，D为PB中点，
∴MD∥AP，
又MD?平面ABC，
∴MD∥平面APC．
（Ⅱ）∵△PMB为正三角形，且D为PB中点，
∴MD⊥PB．
又由（Ⅰ）知MD∥AP，
∴AP⊥PB．
又已知AP⊥PC，PB∩PC=P
∴AP⊥平面PBC，而BC包含于平面PBC，
∴AP⊥BC，
又AC⊥BC，而AP∩AC=A，
∴BC⊥平面APC，
又BC包含于平面ABC
∴平面ABC⊥平面PAC．
∴MD∥AP，
又MD?平面ABC，
∴MD∥平面APC．
（Ⅱ）∵△PMB为正三角形，且D为PB中点，
∴MD⊥PB．
又由（Ⅰ）知MD∥AP，
∴AP⊥PB．
又已知AP⊥PC，PB∩PC=P
∴AP⊥平面PBC，而BC包含于平面PBC，
∴AP⊥BC，
又AC⊥BC，而AP∩AC=A，
∴BC⊥平面APC，
又BC包含于平面ABC
∴平面ABC⊥平面PAC．
练习册系列答案
期末好成绩系列答案
99加1领先期末特训卷系列答案
百强名校期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案
金状元绩优好卷系列答案
相关题目
