题目内容

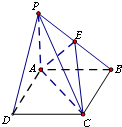
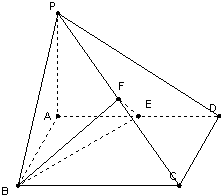
如图，在四棱锥P-ABCD中，底面ABCD是矩形，PA⊥面ABCD，AP=AB=2，BC=2
2
，E、F分别是AD、PC的中点．
（1）求证：EF∥面PAB；
（2）求EF与面ABCD所成角．
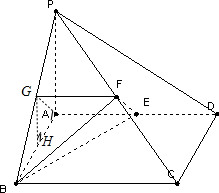
（1）取PB的中点G，连接FG、AG，则FG∥AE，FG=AE
∴四边形AGFE为平行四边形，
∴EF∥AG又EF?面PAB，AG?面PAB，
∴EF∥面PAB．
（2）由（1）知，AG与面ABCD所成角可为所求，
取AB中点H，连接GH，∵PA⊥面ABCD，
∴GH⊥面ABCD，则∠BAG=45°为所求．
练习册系列答案
相关题目
已知正方体ABCD-A1B1C1D1的棱长为1，动点P在正方体ABCD-A1B1C1D1表面上运动，且PA=r（0＜r＜
3
），记点P的轨迹的长度为f（r），则f(
1
2
)=______．（填上所有可能的值）．
如图，在直三棱柱ABC-A1B1C1中，AC=3，AB=5，BC=4，AA1=4，点D是AB的中点，
（1）求证：AC⊥BC1；
（2）求证：AC1∥平面CDB1．
（3）求二面角C1-AB-C的正切值．
已知矩形ABCD，AB=2，BC=x，将△ABD沿矩形的对角线BD所在的直线进行翻折，在翻折过程中，则（　　）
A．当x=1时，存在某个位置，使得AB⊥CD
B．当x=
2
时，存在某个位置，使得AB⊥CD
C．当x=4时，存在某个位置，使得AB⊥CD
D．?x＞0时，都不存在某个位置，使得AB⊥CD
长方体ABCD-A1B1C1D1中，AA1=
2
，AB=BC=2，O是底面对角线的交点．
（Ⅰ）求证：B1D1∥平面BC1D；
（Ⅱ）求证：A1O⊥平面BC1D；
（Ⅲ）求三棱锥A1-DBC1的体积．
在四棱锥P-ABCD中，底面ABCD为边长为4的正方形，PA⊥平面ABCD，E为PB中点，PB=4
2

（Ⅰ）求证：PD∥面ACE；
（Ⅱ）求三棱锥D-AEC的体积．
如图，正方形ABCD和四边形ACEF所在的平面互相垂直．EF∥AC，AB=
2
，CE=EF=1，∠ECA=60°．
（1）求证：AF∥平面BDE；
（2）求异面直线AB与DE所成角的余弦值．
已知AB与CD为异面线段，CD?平面α，AB∥α，M、N分别是线段AC与BD的中点，求证：MN∥平面α．
如图，在正方体ABCD-A1B1C1D1中，AB=1
（1）求异面直线A1B与B1C所成的角；
（2）求证：平面A1BD∥平面B1CD1．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网