题目内容

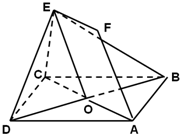
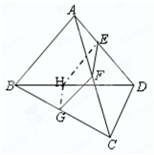
如图，空间四边形ABCD被一平面所截，截面EFGH是平行四边形．
（1）求证：CD∥平面EFGH；
（2）如果AB=CD=a，求证：四边形EFGH的周长为定值．
证明：（1）∵空间四边形ABCD被一平面所截，截面EFGH是平行四边形，
∴EF∥GH，
又∵EF?平面BDC，GH?平面BDC，
∴EF∥平面BDC，
∵EF?平面ADC，
平面ADC∩平面BDC=DC，
∴EF∥DC，又CD?平面EFGH
∴CD∥平面EFGH．
（2）∵空间四边形ABCD被一平面所截，截面EFGH是平行四边形．
AB=CD=a，
∴
AF
AC
=
EF
CD
，
CF
AC
=
FG
AB
，
∴
AF
AC
+
CF
AC
=
EF
CD
+
FG
AB
，
∵AB=CD=a，
AF
AC
+
CF
AC
=1，
EF
CD
+
FG
AB
=
EF+FG
a
，
∴
EF+FG
a
=1，
∴EF+FG=a，
∴四边形EFGH的周长=2a．
故四边形EFGH的周长为定值．
练习册系列答案
相关题目
如图所示，A∉平面α，AB、AC是平面α的两条斜线，O是A在平面α内的射影，AO=4，OC=
3
，BO⊥OC，∠OBA=30°，则C到AB的距离为______．
如图，三角形ABC中，AC=BC=
2
2
AB，ABED是边长为1的正方形，平面ABED⊥底面ABC，若G、F分别是EC、BD的中点．
（Ⅰ）求证：GF∥底面ABC；
（Ⅱ）求证：AC⊥平面EBC；
（Ⅲ）求几何体ADEBC的体积V．
如图，在直三棱柱ABC-A1B1C1中，AC=3，AB=5，BC=4，AA1=4，点D是AB的中点，
（1）求证：AC⊥BC1；
（2）求证：AC1∥平面CDB1．
（3）求二面角C1-AB-C的正切值．
如图，在四棱锥P-ABCD中，底面ABCD是正方形，侧面PAD⊥底面ABCD，且PA⊥PD，E，F分别为PC，BD的中点．证明
（1）EF∥平面PAD；
（2）EF⊥平面PDC．
已知矩形ABCD，AB=2，BC=x，将△ABD沿矩形的对角线BD所在的直线进行翻折，在翻折过程中，则（　　）
A．当x=1时，存在某个位置，使得AB⊥CD
B．当x=
2
时，存在某个位置，使得AB⊥CD
C．当x=4时，存在某个位置，使得AB⊥CD
D．?x＞0时，都不存在某个位置，使得AB⊥CD
长方体ABCD-A1B1C1D1中，AA1=
2
，AB=BC=2，O是底面对角线的交点．
（Ⅰ）求证：B1D1∥平面BC1D；
（Ⅱ）求证：A1O⊥平面BC1D；
（Ⅲ）求三棱锥A1-DBC1的体积．
如图，正方形ABCD和四边形ACEF所在的平面互相垂直．EF∥AC，AB=
2
，CE=EF=1，∠ECA=60°．
（1）求证：AF∥平面BDE；
（2）求异面直线AB与DE所成角的余弦值．
已知正六棱柱ABCDEF-A1B1C1D1E1F1的所有棱长均为2，G为AF的中点．
（1）求证：F1G∥平面BB1E1E；
（2）求证：平面F1AE⊥平面DEE1D1；
（3）求四面体EGFF1的体积．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网