Question

【题目】在平面直角坐标系中，直线的参数方程为（为参数），以坐标原点为极点，轴的正半轴为极轴建立极坐标系，圆的极坐标方程为.

（1）若直线与圆相切，求的值；

（2）直线与圆相交于不同两点，，线段的中点为，求点的轨迹的参数方程.

Answer 1

【答案】（1）或；（2）（为参数，）

【解析】

（1）将圆的极坐标方程转化为直角坐标方程，求得直线的直角坐标方程，根据圆心到直线的距离等于半径列方程，解方程求得直线的斜率，从而求得直线的倾斜角.

（2）根据直线的参数方程，求得三点对应参数的关系，结合韦达定理，求得点的轨迹的参数方程.

（1）∵圆的极坐标方程为，

∴的直角坐标方程为，

圆心为，半径为；

∵直线过点，倾斜角为，

∴当时，不合题意，

当时，斜率为，

则直线的方程为，

即，∵直线与圆相切，

∴，解得，，

即，∴或；

（2）∵直线与圆相交于不同两点，，

∴由（1）知，，

设，，对应的参数分别为，，，

则，

将代入得，

，

则，∴，

又点的坐标满足，

即，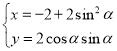

故点的轨迹的参数方程是（为参数，）.