题目内容
平面向量a,b满足|a+2b|= ,且a+2b平行于直线y=2x+1,若b=(2,-1),则a=________.
,且a+2b平行于直线y=2x+1,若b=(2,-1),则a=________.
 ,且a+2b平行于直线y=2x+1,若b=(2,-1),则a=________.
,且a+2b平行于直线y=2x+1,若b=(2,-1),则a=________.(-3,4)或(-5,0)
因为a+2b平行于直线y=2x+1,所以可设a+2b=(m,2m),所以|a+2b|2=5m2=5,解得m=1或-1,a+2b=(1,2)或(-1,-2),所以a=(1,2)-(4-2)=(-3,4)或(-1,-2)-(4,-2)=(-5,0).

练习册系列答案
相关题目
 =λ
=λ ,
,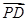 =μ
=μ ,
, =a,
=a,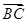 =b.
=b.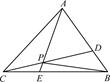
 ;
;

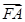 +
+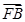 +
+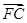 =0,证明:△ABC不可能为直角三角形.
=0,证明:△ABC不可能为直角三角形.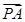 +3
+3 |的最小值为______.
|的最小值为______.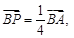 若
若 则
则
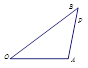
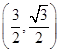 .在△ABC中,
.在△ABC中, =2m+2n,
=2m+2n,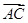 =2m-6n,D为BC边的中点,则|
=2m-6n,D为BC边的中点,则|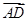 |等于( ).
|等于( ). =a,
=a, =b,
=b,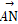 =3
=3 ,M是BC的中点,则
,M是BC的中点,则 = (用a,b表示).
= (用a,b表示). 
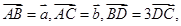 用
用 表示
表示 ,则
,则