题目内容
已知向量α,β,γ满足|α|=1,|α-β|=|β|,(α-γ)·(β-γ)=0.若对每一个确定的β,|γ|的最大值和最小值分别为m,n,则对任意β,m-n的最小值是( )
A. | B.1 | C.2 | D. |
A
方法一,设α=(1,0),β= ,γ=(x,y),由(α-γ)·(β-γ)=0,得(x-1,y)
,γ=(x,y),由(α-γ)·(β-γ)=0,得(x-1,y) =0,即x2-
=0,即x2- x+
x+ +y2-ty=0,配方得
+y2-ty=0,配方得 .|γ|的几何意义是圆上的点到坐标原点的距离,其最大值为圆心到坐标原点的距离加圆的半径,最小值为圆心到坐标原点的距离减去圆的半径,最大值与最小值之差为圆的直径,故m-n=2
.|γ|的几何意义是圆上的点到坐标原点的距离,其最大值为圆心到坐标原点的距离加圆的半径,最小值为圆心到坐标原点的距离减去圆的半径,最大值与最小值之差为圆的直径,故m-n=2  ≥
≥ ,当且仅当t=0时等号成立,此时β=
,当且仅当t=0时等号成立,此时β= .
.
方法二,将向量α,β,γ的起点放在点O,终点分别记作A,B,C.由|α-β|=|β|可知点B在OA的垂直平分线上.根据(α-γ)·(β-γ)=0知点C在以AB为直径的圆上,则m-n为圆的直径.又因为OB=AB,故只要OB最小即得,结合图形,在点B为OA的中点时取得,即m-n的最小值为 .
.

 ,γ=(x,y),由(α-γ)·(β-γ)=0,得(x-1,y)
,γ=(x,y),由(α-γ)·(β-γ)=0,得(x-1,y) =0,即x2-
=0,即x2- x+
x+ +y2-ty=0,配方得
+y2-ty=0,配方得 .|γ|的几何意义是圆上的点到坐标原点的距离,其最大值为圆心到坐标原点的距离加圆的半径,最小值为圆心到坐标原点的距离减去圆的半径,最大值与最小值之差为圆的直径,故m-n=2
.|γ|的几何意义是圆上的点到坐标原点的距离,其最大值为圆心到坐标原点的距离加圆的半径,最小值为圆心到坐标原点的距离减去圆的半径,最大值与最小值之差为圆的直径,故m-n=2  ≥
≥ ,当且仅当t=0时等号成立,此时β=
,当且仅当t=0时等号成立,此时β= .
.方法二,将向量α,β,γ的起点放在点O,终点分别记作A,B,C.由|α-β|=|β|可知点B在OA的垂直平分线上.根据(α-γ)·(β-γ)=0知点C在以AB为直径的圆上,则m-n为圆的直径.又因为OB=AB,故只要OB最小即得,结合图形,在点B为OA的中点时取得,即m-n的最小值为
 .
.

练习册系列答案
相关题目
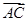 =(1,2),
=(1,2), =(-4,2),则该四边形的面积为( )
=(-4,2),则该四边形的面积为( )

 =λa+b,
=λa+b, =a+μb(λ,μ∈R),那么A,B,C三点共线的充要条件是( )
=a+μb(λ,μ∈R),那么A,B,C三点共线的充要条件是( )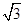 ,-1),则|a-b|的最大值为( )
,-1),则|a-b|的最大值为( ) ,且a+2b平行于直线y=2x+1,若b=(2,-1),则a=________.
,且a+2b平行于直线y=2x+1,若b=(2,-1),则a=________. +
+ )·
)· 等于________.
等于________.
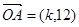 ,
,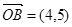 ,
,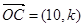 ,且
,且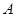 、
、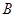 、
、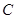 三点共线,
三点共线,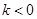 时,若
时,若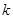 为直线的斜率,则过点
为直线的斜率,则过点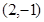 的直线方程为 ;
的直线方程为 ;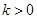 时,若等差数列
时,若等差数列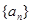 前9项的和等于前4项的和,
前9项的和等于前4项的和,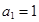 ,则
,则 .
. =(cosθ,sinθ),
=(cosθ,sinθ), =(2+sinθ,2-cosθ),则向量
=(2+sinθ,2-cosθ),则向量 模长的最大值是 .
模长的最大值是 .