题目内容
平面内动点P到点F(1,0)的距离等于它到直线x=-1的距离,记点P的轨迹为曲线Γ.
(1)求曲线Γ的方程;
(2)若点A,B,C是Γ上的不同三点,且满足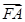 +
+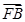 +
+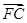 =0,证明:△ABC不可能为直角三角形.
=0,证明:△ABC不可能为直角三角形.
(1)求曲线Γ的方程;
(2)若点A,B,C是Γ上的不同三点,且满足
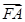 +
+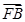 +
+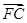 =0,证明:△ABC不可能为直角三角形.
=0,证明:△ABC不可能为直角三角形.(1)y2=4x(2)不可能是直角三角形
(1)由条件可知,点P到点F(1,0)的距离与到直线x=-1的距离相等,所以点P的轨迹是以F(1,0)为焦点,x=-1为准线的抛物线,其方程为y2=4x.
(2)证明:方法一,假设△ABC是直角三角形,且∠A=90°,
A(x1,y1),B(x2,y2),C(x3,y3),则
 =(x2-x1,y2-y1),
=(x2-x1,y2-y1), =(x3-x1,y3-y1),且
=(x3-x1,y3-y1),且 ·
· =0,
=0,
所以(x2-x1)(x3-x1)+(y2-y1)(y3-y1)=0.
因为xi= (i=1,2,3),y1≠y2,y1≠y3,
(i=1,2,3),y1≠y2,y1≠y3,
所以(y1+y2)(y1+y3)+16=0.
又因为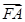 +
+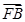 +
+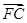 =0,所以x1+x2+x3=3,y1+y2+y3=0,
=0,所以x1+x2+x3=3,y1+y2+y3=0,
所以y2y3=-16,①
又 +
+ +
+ =4(x1+x2+x3)=12,
=4(x1+x2+x3)=12,
所以(-y2-y3)2+ +
+ =12,即
=12,即 +
+ +y2y3=6,②
+y2y3=6,②
由①②得 +
+ -16=6,即
-16=6,即 -22
-22 +256=0,③
+256=0,③
因为Δ=(-22)2-4×256=-540<0.
所以方程③无解,从而△ABC不可能是直角三角形.
方法二,设A(x1,y1),B(x2,y2),C(x3,y3),由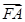 +
+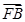 +
+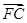 =0,
=0,
得x1+x2+x3=3,y1+y2+y3=0.欲证△ABC不是直角三角形,只需证明∠A≠90°.
(ⅰ)当AB⊥x轴时,x1=x2,y1=-y2,从而x3=3-2x1,y3=0,
即点C的坐标为(3-2x1,0).
由于点C在y2=4x上,所以3-2x1=0,即x1= ,
,
此时A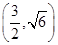 ,B
,B ,C(0,0),则∠A≠90°.
,C(0,0),则∠A≠90°.
(ⅱ)当AB与x轴不垂直时,设直线AB的方程为x=ty+m(t≠0),代入y2=4x,整理得y2-4ty-4m=0,则y1+y2=4t.
若∠A=90°,则直线AC的斜率为-t,同理可得y1+y3=- .
.
由y1+y2+y3=0,得y1=4t- ,y2=
,y2= ,y3=-4t.
,y3=-4t.
由x1+x2+x3=3,可得 +
+ +
+ =4(x1+x2+x3)=12.
=4(x1+x2+x3)=12.
从而 +
+ +(-4t)2=12,
+(-4t)2=12,
整理得t2+ =
= ,即8t4-11t2+8=0,④
,即8t4-11t2+8=0,④
Δ=(-11)2-4×8×8=-135<0.
所以方程④无解,从而∠A≠90°.
综合(ⅰ)(ⅱ)可知,△ABC不可能是直角三角形.
(2)证明:方法一,假设△ABC是直角三角形,且∠A=90°,
A(x1,y1),B(x2,y2),C(x3,y3),则
 =(x2-x1,y2-y1),
=(x2-x1,y2-y1), =(x3-x1,y3-y1),且
=(x3-x1,y3-y1),且 ·
· =0,
=0,所以(x2-x1)(x3-x1)+(y2-y1)(y3-y1)=0.
因为xi=
 (i=1,2,3),y1≠y2,y1≠y3,
(i=1,2,3),y1≠y2,y1≠y3,所以(y1+y2)(y1+y3)+16=0.
又因为
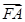 +
+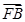 +
+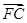 =0,所以x1+x2+x3=3,y1+y2+y3=0,
=0,所以x1+x2+x3=3,y1+y2+y3=0,所以y2y3=-16,①
又
 +
+ +
+ =4(x1+x2+x3)=12,
=4(x1+x2+x3)=12,所以(-y2-y3)2+
 +
+ =12,即
=12,即 +
+ +y2y3=6,②
+y2y3=6,②由①②得
 +
+ -16=6,即
-16=6,即 -22
-22 +256=0,③
+256=0,③因为Δ=(-22)2-4×256=-540<0.
所以方程③无解,从而△ABC不可能是直角三角形.
方法二,设A(x1,y1),B(x2,y2),C(x3,y3),由
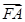 +
+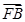 +
+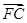 =0,
=0,得x1+x2+x3=3,y1+y2+y3=0.欲证△ABC不是直角三角形,只需证明∠A≠90°.
(ⅰ)当AB⊥x轴时,x1=x2,y1=-y2,从而x3=3-2x1,y3=0,
即点C的坐标为(3-2x1,0).
由于点C在y2=4x上,所以3-2x1=0,即x1=
 ,
,此时A
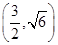 ,B
,B ,C(0,0),则∠A≠90°.
,C(0,0),则∠A≠90°.(ⅱ)当AB与x轴不垂直时,设直线AB的方程为x=ty+m(t≠0),代入y2=4x,整理得y2-4ty-4m=0,则y1+y2=4t.
若∠A=90°,则直线AC的斜率为-t,同理可得y1+y3=-
 .
.由y1+y2+y3=0,得y1=4t-
 ,y2=
,y2= ,y3=-4t.
,y3=-4t.由x1+x2+x3=3,可得
 +
+ +
+ =4(x1+x2+x3)=12.
=4(x1+x2+x3)=12.从而
 +
+ +(-4t)2=12,
+(-4t)2=12,整理得t2+
 =
= ,即8t4-11t2+8=0,④
,即8t4-11t2+8=0,④Δ=(-11)2-4×8×8=-135<0.
所以方程④无解,从而∠A≠90°.
综合(ⅰ)(ⅱ)可知,△ABC不可能是直角三角形.

练习册系列答案
相关题目
 ,求证:a∥b.
,求证:a∥b. 和
和 ,它们的夹角为90°.如图所示,点C在以O为圆心的圆弧
,它们的夹角为90°.如图所示,点C在以O为圆心的圆弧 上运动,若
上运动,若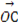 =x
=x
 =λa+b,
=λa+b, =a+μb(λ,μ∈R),那么A,B,C三点共线的充要条件是( )
=a+μb(λ,μ∈R),那么A,B,C三点共线的充要条件是( )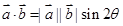 ,(其中
,(其中 为
为 、
、 的夹角),已知△ABC中,
的夹角),已知△ABC中,
 ,则此三角形一定是( )
,则此三角形一定是( ) ,且a+2b平行于直线y=2x+1,若b=(2,-1),则a=________.
,且a+2b平行于直线y=2x+1,若b=(2,-1),则a=________.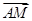 ·
·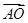 的值为________.
的值为________.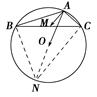
 ,
, ,
, 与
与 的夹角为
的夹角为 ,
, ,则
,则 的夹角为 .
的夹角为 .