题目内容
3.方程$\frac{x^2}{4+m}+\frac{y^2}{2-m}=1$表示椭圆的必要不充分条件是( )| A. | m∈(-1,2) | B. | m∈(-4,2) | C. | m∈(-4,-1)∪(-1,2) | D. | m∈(-1,+∞) |
分析 由条件根据椭圆的标准方程,求得方程$\frac{x^2}{4+m}+\frac{y^2}{2-m}=1$表示椭圆的充要条件所对应的m的范围,则由题意可得所求的m的范围包含所求得的m范围,结合所给的选项,得出结论.
解答 解:方程$\frac{x^2}{4+m}+\frac{y^2}{2-m}=1$表示椭圆的充要分条件是 $\left\{\begin{array}{l}{4+m>0}\\{2-m>0}\\{4+m≠2-m}\end{array}\right.$,即 m∈(-4,-1)∪(-1,2).
由题意可得,所求的m的范围包含集合(-4,-1)∪(-1,2),
故选:B.
点评 本题主要考查椭圆的标准方程,充分条件、必要条件,要条件的定义,属于基础题.

练习册系列答案
 一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案
相关题目
13.在△ABC中,角A,B,C成单调递增的等差数列,a,b,c是的△ABC三边,$b=\frac{{\sqrt{3}}}{2}$,则c-a的取值范围是( )
| A. | $(0,\frac{1}{4})$ | B. | $(0,\frac{{\sqrt{3}}}{2})$ | C. | $(0,\frac{1}{2})$ | D. | ($\frac{1}{4}$,$\frac{\sqrt{3}}{2}$) |
14.已知(1-2x)7=a0+a1x+a2x2+…+a7x7.则|a0|+|a1|+|a2|+…+|a7|=( )
| A. | -1 | B. | 1 | C. | 2187 | D. | -2187 |
11.函数f(x)=$\frac{1}{2}$x2-ln x的最小值( )
| A. | $\frac{1}{2}$ | B. | 1 | C. | 不存在 | D. | 0 |
12.如图是某四棱锥的三视图,则该棱锥的体积是 ( )
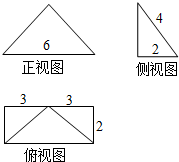

| A. | 48 | B. | 24$\sqrt{3}$ | C. | 16 | D. | 8$\sqrt{3}$ |
 如图是y=f(x)的导函数的图象,现有四种说法:
如图是y=f(x)的导函数的图象,现有四种说法: