题目内容
2.函数f(x)=x+$\frac{1}{x-1}$(x>1)的最小值是3;此时x=2.分析 由x>1可得x-1>0,函数y=$\frac{1}{x-1}$+x=x-1+$\frac{1}{x-1}$+1,利用基本不等式即可得出.
解答 解:∵x>1,∴x-1>0.
∴函数y=$\frac{1}{x-1}$+x=x-1+$\frac{1}{x-1}$+1≥2$\sqrt{(x-1)•\frac{1}{x-1}}$+1=3,
当且仅当x=2时取等号.
∴函数y=$\frac{1}{x-1}$+x的最小值是3.此时x=2.
故答案为:3,2.
点评 本题考查基本不等式的运用:求最值,注意变形:x=x-1+1,属于基础题.

练习册系列答案
 口算小状元口算速算天天练系列答案
口算小状元口算速算天天练系列答案 天天练口算系列答案
天天练口算系列答案
相关题目
12.如图是某四棱锥的三视图,则该棱锥的体积是 ( )
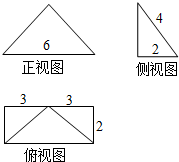

| A. | 48 | B. | 24$\sqrt{3}$ | C. | 16 | D. | 8$\sqrt{3}$ |
17.在△ABC中AC=BC=3,AB=2,P为三角形ABC内切圆圆周上一点,则$\overrightarrow{PA}•\overrightarrow{PB}$的最大值与最小值之差为( )
| A. | 4 | B. | 2$\sqrt{3}$ | C. | 2$\sqrt{2}$ | D. | 2 |
7.设m∈R,不等式mx2-(3m+1)x+2(m+1)>0的解集记为集合P.
(I)若P=(x|-1<x<2),求m的值;
(Ⅱ)当m>0时,求集合P;
(Ⅲ)若{x|-3<x<2}⊆P,求m的取值范围.
(I)若P=(x|-1<x<2),求m的值;
(Ⅱ)当m>0时,求集合P;
(Ⅲ)若{x|-3<x<2}⊆P,求m的取值范围.
14.若A${\;}_{n}^{2}$=4C${\;}_{n-1}^{2}$,则n的值为( )
| A. | 7 | B. | 6 | C. | 5 | D. | 4 |