题目内容
4. 如图所示,在平面四边形ABCD中,$\overrightarrow{DA}•\overrightarrow{AB}=0,|{\overrightarrow{EC}}|=\sqrt{7},|{\overrightarrow{AD}}|=3,\overrightarrow{AE}=2\overrightarrow{ED}$,$\overrightarrow{DA}$与$\overrightarrow{DC}$的夹角为$\frac{2}{3}π$,$\overrightarrow{EC}$与$\overrightarrow{EB}$的夹角为$\frac{π}{3}$.
如图所示,在平面四边形ABCD中,$\overrightarrow{DA}•\overrightarrow{AB}=0,|{\overrightarrow{EC}}|=\sqrt{7},|{\overrightarrow{AD}}|=3,\overrightarrow{AE}=2\overrightarrow{ED}$,$\overrightarrow{DA}$与$\overrightarrow{DC}$的夹角为$\frac{2}{3}π$,$\overrightarrow{EC}$与$\overrightarrow{EB}$的夹角为$\frac{π}{3}$.(1)求△CDE的面积S;
(2)求$|{\overrightarrow{BE}}|$.
分析 (1)由题意可得DA⊥AB,DE=1,EC=$\sqrt{7}$,EA=2,∠ADC=$\frac{2π}{3}$,∠BEC=$\frac{π}{3}$.设∠CED=α.运用余弦定理和正弦定理,再由面积公式,即可得到所求S;
(2)求得cosα,以及cos∠AEB=cos($\frac{2π}{3}$-α),再由解直角三角形,即可得到所求.
解答 解:由题意可知:DA⊥AB,DE=1,EC=$\sqrt{7}$,EA=2,
∠ADC=$\frac{2π}{3}$,∠BEC=$\frac{π}{3}$.
设∠CED=α.
(1)在△CDE中,由余弦定理,得
EC2=CD2+DE2-2CD•DE•cos∠EDC,
于是由题设知,7=CD2+1+CD,即CD2+CD-6=0,
解得CD=2(CD=-3舍去).
在△CDE中,由正弦定理,得$\frac{EC}{sin∠EDC}=\frac{CD}{sinα}$,
于是,sinα=$\frac{CD•sin∠EDC}{EC}$=$\frac{2×\frac{\sqrt{3}}{2}}{\sqrt{7}}$=$\frac{\sqrt{21}}{7}$,
即sin∠CED=$\frac{\sqrt{21}}{7}$.
于是,$S=\frac{1}{2}DE•EC•sinα=\frac{1}{2}×\sqrt{7}×\frac{{\sqrt{21}}}{7}=\frac{{\sqrt{3}}}{2}$;
(2)由题设知,0<α<$\frac{π}{3}$,于是由(1)知,
cosα=$\sqrt{1-{{sin}^2}α}$=$\sqrt{1-\frac{21}{49}}$=$\frac{2\sqrt{7}}{7}$.
而∠AEB=$\frac{2π}{3}$-α,
所以cos∠AEB=cos($\frac{2π}{3}$-α)=cos$\frac{2π}{3}$cosα+sin$\frac{2π}{3}$sinα
=-$\frac{1}{2}$cosα+$\frac{\sqrt{3}}{2}$sinα
=-$\frac{1}{2}$×$\frac{2\sqrt{7}}{7}$+$\frac{\sqrt{3}}{2}$×$\frac{\sqrt{21}}{7}$=$\frac{\sqrt{7}}{14}$.
在Rt△EAB中,cos∠AEB=$\frac{EA}{BE}$=$\frac{2}{BE}$,
故$|{\overrightarrow{BE}}|$=BE=$\frac{2}{cos∠AEB}$=$\frac{2}{\frac{\sqrt{7}}{14}}$=4$\sqrt{7}$.
点评 本题主要考查余弦定理和正弦定理、面积公式的运用,同时考查向量垂直的条件,同角公式和两角差的余弦公式,属于中档题.

| A. | -1 | B. | 1 | C. | 2187 | D. | -2187 |
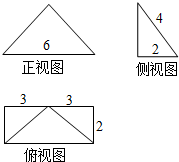
| A. | 48 | B. | 24$\sqrt{3}$ | C. | 16 | D. | 8$\sqrt{3}$ |
| A. | 7 | B. | 6 | C. | 5 | D. | 4 |
