题目内容
17.已知函数f(x)=Asin(ωx+φ)(ω>0),如果存在实数x1使得对任意的实数x,都有f(x1)≤f(x)≤f(x1+2015)成立,则ω的最小值为( )
| A. | $\frac{π}{2015}$ | B. | $\frac{1}{2015}$ | C. | $\frac{π}{4010}$ | D. | $\frac{1}{4010}$ |
分析 由题意可得区间[x1,x1+2015]能够包含函数的至少一个完整的单调区间,即2015≥$\frac{1}{2}$•$\frac{2π}{ω}$,解得即可.
解答 解:显然要使结论成立,只需保证区间[x1,x1+2015]能够包含函数的至少一个完整的单调区间即可,
又∵f(x)=Asin(ωx+φ)(ω>0),则2015≥$\frac{1}{2}$•$\frac{2π}{ω}$,
∴ω≥$\frac{π}{2015}$,
则ω的最小值为:$\frac{π}{2015}$,
故选:A.
点评 本题主要考查正弦函数的单调性和周期性,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
8.函数f(x)=ex-ax-1在R上单调递增,则实数a的取值范围为( )
| A. | R | B. | [0,+∞) | C. | (-∞,0] | D. | [-1,1] |
9.函数f(x)=-cosx•lg|x|的部分图象是( )
| A. | 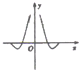 | B. | 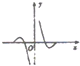 | C. | 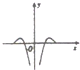 | D. | 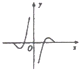 |