题目内容
【题目】已知抛物线![]() :
: ![]() 的焦点为
的焦点为![]() ,圆
,圆![]() :
: ![]() .直线
.直线![]() 与抛物线
与抛物线![]() 交于点
交于点![]() 、
、![]() 两点,与圆
两点,与圆![]() 切于点
切于点![]() .
.
(1)当切点![]() 的坐标为
的坐标为![]() 时,求直线
时,求直线![]() 及圆
及圆![]() 的方程;
的方程;
(2)当![]() 时,证明:
时,证明: ![]() 是定值,并求出该定值.
是定值,并求出该定值.
【答案】(1)圆![]() :
: ![]() ,直线
,直线![]() :
: ![]() (或
(或![]() );
);
或圆![]() :
: ![]() ,直线
,直线![]() :
: ![]() (或
(或![]() ).(2)定值为
).(2)定值为![]() .
.
【解析】试题分析:(1)将![]() 代入圆方程,即可求得
代入圆方程,即可求得![]() 的值,根据圆的方程求得圆心,再根据直线的斜率公式求得
的值,根据圆的方程求得圆心,再根据直线的斜率公式求得![]() 的斜率
的斜率![]() ,则直线
,则直线![]() 的方程斜率为
的方程斜率为![]() ,利用直线的点斜式方程,即可求得
,利用直线的点斜式方程,即可求得![]() 的方程;
的方程;
(2)将当![]() 垂直与
垂直与![]() 轴时,求得
轴时,求得![]() 和
和![]() 点坐标,利用两点之间的斜率公式,即可求得
点坐标,利用两点之间的斜率公式,即可求得![]() 的值;当
的值;当![]() 不垂直于
不垂直于![]() 轴时,由直线
轴时,由直线![]() 与圆
与圆![]() 相切,求得
相切,求得![]() ,将直线
,将直线![]() 代入抛物线方程.利用韦达定理及弦长公式求得
代入抛物线方程.利用韦达定理及弦长公式求得![]() ,利用抛物线的定义,
,利用抛物线的定义, ![]() ,即可求得
,即可求得![]() 是定值.
是定值.
试题解析:
(1)把点![]() 代入圆
代入圆![]() 的方程可得:
的方程可得:
![]()
![]() 或
或![]() .
.
(i)当![]() 时,圆
时,圆![]() .∴圆心
.∴圆心![]() ,
, 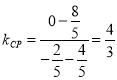 ,
,
∴![]() ,∴
,∴![]() 的方程为:
的方程为: ![]() ,化简得:
,化简得: ![]() .
.
(ii)当![]() 时,圆
时,圆![]() ,∴圆心
,∴圆心![]() ,
, 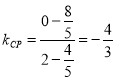 ,
,
∴![]() ,∴
,∴![]() 的方程为:
的方程为: ![]() ,化简得:
,化简得: ![]() .
.
综上所述,圆![]() ,直线
,直线![]() (或
(或![]() );
);
或圆![]() ,直线
,直线![]() (或
(或![]() ).
).
(2)![]() 时,由(1)知,圆
时,由(1)知,圆![]() .
.
(i)当![]() 垂直于
垂直于![]() 轴时,
轴时, ![]() ,
, ![]() ,
, ![]() ,
,
∴![]() ,
, ![]() .∴
.∴![]() .
.
(ii)当直线![]() 不垂直于
不垂直于![]() 轴时,设直线
轴时,设直线![]() .
.
∵直线![]() 与圆
与圆![]() 相切.∴
相切.∴![]() ,∴
,∴![]() ,
, ![]() .
.
联立直线![]() 与抛物线
与抛物线![]() ,得
,得![]()
![]() .
.
∴![]()
![]()
![]() .
.
又∵![]() ,
, ![]() ,
,
∴![]()
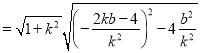
![]()
![]()
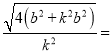
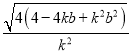
![]() .
.
由抛物线的性质可知, ![]()
![]() ,
,
∴![]() ,∴
,∴![]() .
.
综上所述, ![]() 是定值,且该定值为2.
是定值,且该定值为2.

【题目】为了研究家用轿车在高速公路上的车速情况,交通部门对![]() 名家用轿车驾驶员进行调查,得到其在高速公路上行驶时的平均车速情况为:在
名家用轿车驾驶员进行调查,得到其在高速公路上行驶时的平均车速情况为:在![]() 名男性驾驶员中,平均车速超过
名男性驾驶员中,平均车速超过![]()
![]() 的有
的有![]() 人,不超过
人,不超过![]()
![]() 的有
的有![]() 人;在
人;在![]() 名女性驾驶员中,平均车速超过
名女性驾驶员中,平均车速超过![]()
![]() 的有
的有![]() 人,不超过
人,不超过![]()
![]() 的有
的有![]() 人.
人.
(Ⅰ)完成下面的列联表,并判断是否有![]() 的把握认为平均车速超过100
的把握认为平均车速超过100![]() 与性别有关;
与性别有关;
平均车速超过 | 平均车速不超过 | 合计 | |
男性驾驶人数 | |||
女性驾驶人数 | |||
合计 |
(Ⅱ)在被调查的驾驶员中,按分层抽样的方法从平均车速不超过![]()
![]() 的人中抽取
的人中抽取![]() 人,再从这
人,再从这![]() 人中采用简单随机抽样的方法随机抽取
人中采用简单随机抽样的方法随机抽取![]() 人,求这
人,求这![]() 人恰好为
人恰好为![]() 名男生、
名男生、![]() 名女生的概率.
名女生的概率.
参考公式与数据:![]() ,其中
,其中![]() .
.
| 0.150 | 0.100 | 0.050 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
