Question

【题目】已知椭圆 的离心率为，以原点为圆心，椭圆C的短半轴长为半径的圆与直线相切.、是椭圆的左、右顶点，直线过点且与轴垂直.

（1）求椭圆的标准方程；

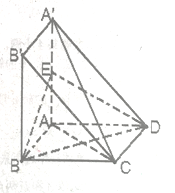
（2）设是椭圆上异于、的任意一点，作轴于点，延长到点使得，连接并延长交直线于点，为线段的中点，判断直线与以为直径的圆的位置关系，并证明你的结论.

Answer 1

【答案】（Ⅰ）；（Ⅱ）相切．

【解析】试题分析：(1)根据点到直线距离公式得 ,再根据离心率得 (2) 设，依次得Q,M,N坐标，即得QN方程，再利用点到直线距离公式得圆心到直线距离，最后根据圆心到直线距离与半径关系确定直线与以为直径的圆的位置关系

试题解析：（Ⅰ）由题意：到直线的距离为，则

椭圆C的标准方程为

（Ⅱ）设，则

直线的方程为

与联立得：

则直线的方程为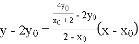

即

方程可化为

到直线的距离为

故直线与以AB为直径的圆O相切.