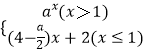题目内容
【题目】已知椭圆![]() 与抛物线
与抛物线![]() 共焦点
共焦点![]() ,抛物线上的点M到y轴的距离等于
,抛物线上的点M到y轴的距离等于![]() ,且椭圆与抛物线的交点Q满足
,且椭圆与抛物线的交点Q满足![]() .
.
(I)求抛物线的方程和椭圆的方程;
(II)过抛物线上的点![]() 作抛物线的切线
作抛物线的切线![]() 交椭圆于
交椭圆于![]() 、
、![]() 两点,设线段AB的中点为
两点,设线段AB的中点为![]() ,求
,求![]() 的取值范围.
的取值范围.
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】试题分析:(1)将抛物线上的点![]() 到
到![]() 轴的距离等于
轴的距离等于![]() 和抛物线的定义相结合,可得
和抛物线的定义相结合,可得![]() ,可得抛物线的方程,已知在椭圆中
,可得抛物线的方程,已知在椭圆中![]() 的值,由
的值,由![]() 可得点Q的坐标,结合椭圆的定义可得椭圆的方程;(2)联立直线与抛物线的方程,结合其有一个交点可得关系式
可得点Q的坐标,结合椭圆的定义可得椭圆的方程;(2)联立直线与抛物线的方程,结合其有一个交点可得关系式![]() ,联立直线与椭圆的方程根据椭圆与直线有2个交点即
,联立直线与椭圆的方程根据椭圆与直线有2个交点即![]() ,得到关于
,得到关于![]() 不等式,解不等式可得
不等式,解不等式可得![]() 的取值范围,由中点坐标公式及韦达定理可得
的取值范围,由中点坐标公式及韦达定理可得![]() ,从而可得其范围.
,从而可得其范围.
试题解析:(1)∵抛物线上的点![]() 到
到![]() 轴的距离等于
轴的距离等于![]() ,
,
∴点M到直线![]() 的距离等于点
的距离等于点![]() 到焦点
到焦点![]() 的距离,
的距离,
得![]() 是抛物线
是抛物线![]() 的准线,即
的准线,即![]() ,
,
解得![]() ,∴抛物线的方程为
,∴抛物线的方程为![]() ;
;
可知椭圆的右焦点![]() ,左焦点
,左焦点![]() ,
,
由![]() 得
得![]() ,又
,又![]() ,解得
,解得![]() ,
,
由椭圆的定义得![]() ,
,
∴![]() ,又
,又![]() ,得
,得![]() ,
,
∴椭圆的方程为![]() .
.
(2)显然![]() ,
, ![]() ,
,
由![]() ,消去
,消去![]() ,得
,得![]() ,
,
由题意知![]() ,得
,得![]() ,
,
由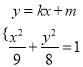 ,消去
,消去![]() ,得
,得![]() ,
,
其中![]() ,
,
化简得![]() ,
,
又![]() ,得
,得![]() ,解得
,解得![]() ,
,
设![]() ,则
,则![]() <0,
<0,
由![]() ,得
,得![]() ,∴
,∴![]() 的取值范围是
的取值范围是![]() .
.

 阅读快车系列答案
阅读快车系列答案【题目】某研究小组在电脑上进行人工降雨模拟实验,准备用A、B、C三种人工降雨方式分别对甲、乙、丙三地实施人工降雨,其实验统计结果如下
方式 | 实施地点 | 大雨 | 中雨 | 小雨 | 模拟实验次数 |
A | 甲 | 2次 | 6次 | 4次 | 12次 |
B | 乙 | 3次 | 6次 | 3次 | 12次 |
C | 丙 | 2次 | 2次 | 8次 | 12次 |
假定对甲、乙、丙三地实施的人工降雨彼此互不影响,且不考虑洪涝灾害,请根据统计数据:
(1)求甲、乙、丙三地都恰为中雨的概率;
(2)考虑不同地区的干旱程度,当雨量达到理想状态时,能缓解旱情,若甲、丙地需中雨或大雨即达到理想状态,乙地必须是大雨才达到理想状态,记“甲、乙、丙三地中缓解旱情的个数”为随机变量![]() ,求
,求![]() 的分布列和数学期望.
的分布列和数学期望.
【题目】为了普及环保知识,增强环保意识,某校从理科甲班抽取60人,从文科乙班抽取50人参加环保知识测试.
优秀人数 | 非优秀人数 | 总计 | |
甲班 | |||
乙班 | 30 | ||
总计 | 60 |
(Ⅰ)根据题目完成![]() 列联表,并据此判断是否有
列联表,并据此判断是否有![]() 的把握认为环保知识成绩优秀与学生的文理分类有关.
的把握认为环保知识成绩优秀与学生的文理分类有关.
(Ⅱ)现已知![]() ,
, ![]() ,
, ![]() 三人获得优秀的概率分别为
三人获得优秀的概率分别为![]() ,
, ![]() ,
, ![]() ,设随机变量
,设随机变量![]() 表示
表示![]() ,
, ![]() ,
, ![]() 三人中获得优秀的人数,求
三人中获得优秀的人数,求![]() 的分布列及期望
的分布列及期望![]() .
.
附:  ,
, ![]()
| 0.100 | 0.050 | 0.025 | 0.010 | 0.005 |
| 2.706 | 3.841 | 5.024 | 6.635 | 7.879 |