题目内容
5.已知函数f(θ)=2sin($\frac{π}{4}$+θ)[$\sqrt{3}$sin($\frac{π}{4}$+θ)+cos($\frac{π}{4}$+θ)],设角A为△ABC的内角,满足f(A)=$\sqrt{3}$+1.(1)求角A的大小;
(2)若a=3,BC边上的中线长为3,求△ABC的面积.
分析 (1)把已知由同角三角函数的基本关系式化简,代入f(A)=$\sqrt{3}$+1,结合A的范围求解A的值;
(2)分别在三角形ABC、三角形ADB、三角形ADC中运用余弦定理结合已知条件求得AB•AC的值,代入三角形的面积公式得答案.
解答 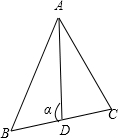 解:f(θ)=2sin($\frac{π}{4}$+θ)[$\sqrt{3}$sin($\frac{π}{4}$+θ)+cos($\frac{π}{4}$+θ)]
解:f(θ)=2sin($\frac{π}{4}$+θ)[$\sqrt{3}$sin($\frac{π}{4}$+θ)+cos($\frac{π}{4}$+θ)]
=2$\sqrt{3}$sin2($\frac{π}{4}$+θ)+2sin($\frac{π}{4}$+θ)cos($\frac{π}{4}$+θ)
=$\sqrt{3}$[1-cos($\frac{π}{2}$+2θ)]+sin($\frac{π}{2}$+2θ)
=$\sqrt{3}$+$\sqrt{3}$sin2θ+cos2θ
=$\sqrt{3}$+2sin(2θ+$\frac{π}{6}$).
(1)由f(A)=$\sqrt{3}$+1,A∈(0,π),得$\sqrt{3}$+2sin(2A+$\frac{π}{6}$)=$\sqrt{3}$+1,
可得:sin(2A+$\frac{π}{6}$)=$\frac{1}{2}$,
∵A∈(0,π),∴A=$\frac{π}{3}$;
(2)如图,
在△ABC中,设BC中点为D,∠ADB=α,则∠ADC=π-α,
则BC2=AC2+AB2-2AB•ACcos$\frac{π}{3}$,
AB2=AD2+BD2-2AD•BDcosα,
AC2=AD2+DC2-2AD•DCcos(π-α),
又AD=3,BD=DC=$\frac{3}{2}$,
联立以上各式求得:AB•AC=$\frac{27}{2}$.
∴S△ABC=$\frac{1}{2}$AB•ACsin$\frac{π}{3}$=$\frac{1}{2}$×$\frac{27}{2}$×$\frac{\sqrt{3}}{2}$=$\frac{27\sqrt{3}}{8}$.
点评 本题考查了同角三角函数的基本关系式,考查了余弦定理在解三角形中的应用,考查了学生的计算能力,是中档题.

 小天才课时作业系列答案
小天才课时作业系列答案 一课四练系列答案
一课四练系列答案 黄冈小状元满分冲刺微测验系列答案
黄冈小状元满分冲刺微测验系列答案 新辅教导学系列答案
新辅教导学系列答案 阳光同学一线名师全优好卷系列答案
阳光同学一线名师全优好卷系列答案| A. | 160 | B. | 180 | C. | 200 | D. | 220 |
| A. | $\frac{3}{4}$ | B. | -$\frac{3}{4}$ | C. | ±$\frac{4}{5}$ | D. | $\frac{4}{5}$ |
| ξ | 1 | 2 | 3 |
| p | $\frac{1}{2}$ | t | $\frac{1}{3}$ |
| A. | $\frac{11}{6}$ | B. | $\frac{15}{2}$ | C. | $\frac{11}{2}$ | D. | $\frac{33}{2}$ |
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |