题目内容
14.已知随机变量ξ的分布列如图所示,若η=3ξ+2,则Eη=( )| ξ | 1 | 2 | 3 |
| p | $\frac{1}{2}$ | t | $\frac{1}{3}$ |
| A. | $\frac{11}{6}$ | B. | $\frac{15}{2}$ | C. | $\frac{11}{2}$ | D. | $\frac{33}{2}$ |
分析 通过概率和为1,求出t,然后求解期望即可.
解答 解:由分布列的概率和为1,可知:$\frac{1}{2}+t+\frac{1}{3}=1$,可得t=$\frac{1}{6}$,
Eξ=$1×\frac{1}{2}+2×\frac{1}{6}+3×\frac{1}{3}$=$\frac{11}{6}$,
η=3ξ+2,
Eη=3Eξ+2=3×$\frac{11}{6}+2$=$\frac{15}{2}$.
故选:B.
点评 本题考查离散型随机变量的分布列以及期望的求法,考查计算能力.

练习册系列答案
相关题目
4.命题“?x∈[0,+∞),x3+x≥0”的否定是( )
| A. | ?x∈(-∞,0),x3+x<0 | B. | ?x0∈[0,+∞),x${\;}_{0}^{3}$+x0<0 | ||
| C. | ?x∈(-∞,0),x3+x≥0 | D. | ?x0∈[0,+∞),x${\;}_{0}^{3}$+x0≥0 |
2.执行如图所示的程序框图,输出的S的值为( )
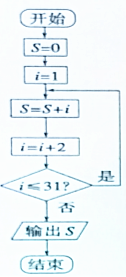

| A. | 256 | B. | 254 | C. | 258 | D. | 252 |