题目内容

10．已知角α是三角形的内角，且tanα+$\frac{1}{tanα}$=-$\frac{10}{3}$，则cos2α=（　　）
A．$\frac{3}{4}$B．-$\frac{3}{4}$C．±$\frac{4}{5}$D．$\frac{4}{5}$

分析 由条件可得α为钝角，sin2α=-$\frac{3}{5}$．再根据同角三角函数的基本关系，以及三角函数在各个象限中的符号，求得cos2α的值．

解答 解：∵角α是三角形的内角，且tanα+$\frac{1}{tanα}$=-$\frac{10}{3}$，则α为钝角，且$\frac{sinα}{cosα}$+$\frac{cosα}{sinα}$=$\frac{1}{sinαcosα}$=$\frac{2}{sin2α}$=-$\frac{10}{3}$，
求得sin2α=-$\frac{3}{5}$．
再结合2α∈（π，2π），可得cos2α=±$\sqrt{{1-sin}^{2}2α}$=±$\frac{4}{5}$，
故选：C．

点评 本题主要考查同角三角函数的基本关系，以及三角函数在各个象限中的符号，属于基础题．

练习册系列答案
相关题目
20．设y=x-lnx，则此函数在区间（0，1）内为（　　）
A．单调递增B．单调递减C．有增有减D．不确定
1．设函数f（x）=a1x+a2x2+a3x3+…+anxn（x∈R，n∈N*），且对一切正整数n都有f（1）=n2成立
（1）求数列{an}的通项公式；
（2）求数列{$\frac{1}{{a}_{n}{a}_{n+1}}$}的前n项和Pn；
（3）求证：f（$\frac{1}{3}$）＜1
（4）设数列{$\frac{1}{{{a}_{n}}^{2}}$}的前n项和为Rn，求证：Rn≤$\frac{3}{2}$-$\frac{1}{4n-2}$．
18．已知抛物线y2=4$\sqrt{2}$x的焦点为椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1（a＞b＞0）的右焦点，且椭圆的长轴长为4，左右顶点分别为A，B．经过椭圆左焦点的直线l与椭圆交于C、D两点．
（Ⅰ）求椭圆标准方程；
（Ⅱ）记△ABD与△ABC的面积分别为S1和S2，且|S1-S2|=2，求直线l的方程；
（Ⅲ）若M（x1，y1），N（x2，y2）是椭圆上的两动点，且满足x1x2+2y1y2=0，动点P满足$\overrightarrow{OP}$=$\overrightarrow{OM}$+2$\overrightarrow{ON}$（其中O为坐标原点），求动点P的轨迹方程．
5．已知函数f（θ）=2sin（$\frac{π}{4}$+θ）[$\sqrt{3}$sin（$\frac{π}{4}$+θ）+cos（$\frac{π}{4}$+θ）]，设角A为△ABC的内角，满足f（A）=$\sqrt{3}$+1．
（1）求角A的大小；
（2）若a=3，BC边上的中线长为3，求△ABC的面积．
15．已知数列{an}、{bn}满足：a1=4，an+1=$\sqrt{{a}_{n}+2}$，bn=an-1（n∈N*）．
（1）判断并证明数列{an}的单调性；
（2）是否存在常数λ，使得b1b2b3…bn＜λ？若存在，求λ的最小值；若不存在，请说明理由．
2．执行如图所示的程序框图，输出的S的值为（　　）
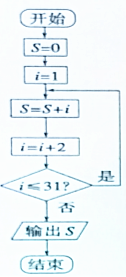
A．256B．254C．258D．252
19．已知F1，F2是椭圆$\frac{{x}^{2}}{4}$+$\frac{{y}^{2}}{3}$=1的两焦点，P为椭圆上一点，△PF1F2的面积为$\sqrt{3}$，求∠F1PF2的大小．
20．已知△ABC中，$\overrightarrow{AB}+\overrightarrow{AC}=λ（\frac{{\overrightarrow{AB}}}{{|\overrightarrow{AB}|}}+\frac{{\overrightarrow{AC}}}{{|\overrightarrow{AC}|}}）$，则三角形的形状一定是（　　）
A．等腰三角形B．等边三角形C．直角三角形D．等腰直角三角形

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网