题目内容
10.已知数列{an}满足:a1+a2+a3+…+an=n-an,n∈N*.(Ⅰ)求证:数列{an-1}是等比数列;
(Ⅱ)令bn=(2-n)(an-1)(n∈N*),若对于?n∈N*,都有bn≤$\frac{1}{4}$sinx,求实数x的取值范围.
分析 (Ⅰ)根据数列的递推关系,结合等比数列的定义进行构造即可证明数列{an-1}是等比数列;
(Ⅱ)先求出数列{an}的通项公式,判断数列{bn}的单调性和最值将不等式进行转化即可得到结论.
解答 证明:(Ⅰ)∵a1+a2+a3+…+an=n-an,n∈N*.
∴a1+a2+a3+…+an+1=n+1-an+1,n∈N*.
两式相减得an+1=1-an+1+an,
即2an+1=1+an,
则an+1-1=$\frac{1}{2}$(an-1),
即数列{an-1}是等比数列,公比q=$\frac{1}{2}$;
当n=1时,a1=1-a1,解得a1=$\frac{1}{2}$,
则首项a1-1=$\frac{1}{2}-1$=$-\frac{1}{2}$,
即数列{an-1}是等比数列成立;
(Ⅱ)由(Ⅰ)知an-1=$-\frac{1}{2}$$•(\frac{1}{2})^{n-1}$=-($\frac{1}{2}$)n,
则bn=(2-n)(an-1)=$\frac{n-2}{{2}^{n}}$,
则bn+1-bn=$\frac{n+1-2}{{2}^{n+1}}$-$\frac{n-2}{{2}^{n}}$=$\frac{3-n}{{2}^{n+1}}$,
当n<3时,bn+1-bn>0,即b1<b2<b3,
当n=3时,bn+1=bn,即b3=b4,
当n>3时,bn+1-bn<0,即b4>b5>b6…,
∴{bn}的最大项为b3=b4=$\frac{1}{8}$,
若对于?n∈N*,都有bn≤$\frac{1}{4}$sinx,则等价为若对于?n∈N*,都有(bn)max≤$\frac{1}{4}$sinx,
即$\frac{1}{8}$≤$\frac{1}{4}$sinx,
即sinx$≥\frac{1}{2}$,即2kπ≤x≤2kπ,2kπ+$\frac{π}{6}$≤x≤2kπ+$\frac{5π}{6}$,k∈Z,
即实数x的取值范围是{x|2kπ+$\frac{π}{6}$≤x≤2kπ+$\frac{5π}{6}$,k∈Z}.
点评 本题主要考查等比数列的判断以及递推数列的应用,考查学生的运算和推理能力.

 名校课堂系列答案
名校课堂系列答案| A. | 2 | B. | $\frac{2\sqrt{3}}{3}$ | C. | $\sqrt{3}$ | D. | $\frac{4\sqrt{3}}{3}$ |
| A. | a≥1 | B. | a>1 | C. | a≤1 | D. | a<2 |
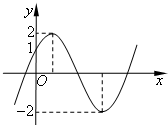 如题图,已知函数$f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<\frac{π}{2})$的图象与y的交点为(0,1),它在y轴右侧的第一个最高点和第一个最低点之间的距离为2$\sqrt{4+{π^2}}$.
如题图,已知函数$f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<\frac{π}{2})$的图象与y的交点为(0,1),它在y轴右侧的第一个最高点和第一个最低点之间的距离为2$\sqrt{4+{π^2}}$.