题目内容
已知定义在R上的函数f(x)对任意实数x、y恒有f(x)+f(y)=f(x+y),且当x>0时,f(x)<0,又f(1)=- .
.
(1)求证:f(x)为奇函数; (2)求证:f(x)在R上是减函数;
(3)求f(x)在[-3,6]上的最大值与最小值.
 .
.(1)求证:f(x)为奇函数; (2)求证:f(x)在R上是减函数;
(3)求f(x)在[-3,6]上的最大值与最小值.
(1)见解析;(2)见解析;(3)最大值为2,最小值为-4
试题分析:(1)欲证函数
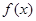 为奇函数,需寻找
为奇函数,需寻找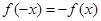 关系.由题中条件可知,需要从f(x)+f(y)=f(x+y)拼凑出
关系.由题中条件可知,需要从f(x)+f(y)=f(x+y)拼凑出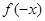 与
与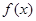 ,令
,令 ,便有
,便有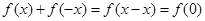 ,需求得
,需求得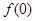 ,考虑到
,考虑到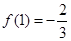 ,令特殊值求
,令特殊值求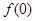 ;(2)同一样的思想,这里需要拼凑出
;(2)同一样的思想,这里需要拼凑出 与
与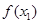 (
(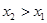 )不等于关系(需利用当x>0时,f(x)<0);(3)利用(1),(2)结论解(3).
)不等于关系(需利用当x>0时,f(x)<0);(3)利用(1),(2)结论解(3).试题解析:令
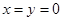 ,可得
,可得 从而
从而 .
.令
 ,可得
,可得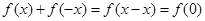 ,即
,即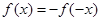 ,
,故
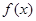 为奇函数. 4分
为奇函数. 4分证明:设
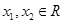 ,且
,且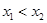 ,则
,则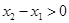 ,于是
,于是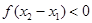 .
.从而
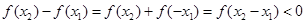 .
.所以
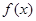 为减函数. 8分
为减函数. 8分解:由(2)知,所求函数的最大值为
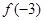 ,最小值为
,最小值为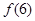 .
.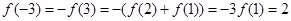 ,
,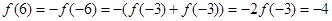 .
.于是
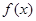 在
在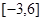 上的最大值为2,最小值为-4. 12分
上的最大值为2,最小值为-4. 12分
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
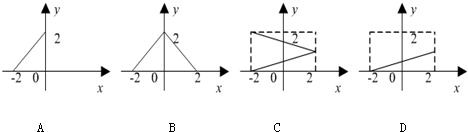
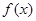 的定义域为
的定义域为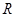 ,
,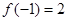 ,对任意
,对任意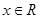 ,
,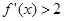 ,则
,则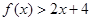 的解
的解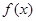 的图像关于点
的图像关于点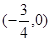 成中心对称且对任意的实数
成中心对称且对任意的实数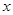 都有
都有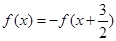 且
且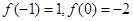 ,则
,则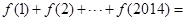 ( ).
( ).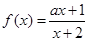 在
在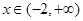 上单调递减,则实数
上单调递减,则实数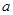 的取值范围是 .
的取值范围是 .