题目内容
函数f(x)=2+3x2-x3在区间[-2,2]上的值域为( )
| A.[2,22] | B.[6,22] | C.[0,20] | D.[6,24] |
对函数求导可得,f′(x)=6x-3x2=3x(2-x)
令f′(x)>0可得,0<x<2
令f′(x)<0可得,-2≤x<0
∴函数f(x)在[-2,0)上单调递减,在(0,2)上单调递增
∴当x=0时,函数有最小值f(0)=2
∵f(2)=6,f(-2)=22
当x=-2时,函数有最大值22
故选A
令f′(x)>0可得,0<x<2
令f′(x)<0可得,-2≤x<0
∴函数f(x)在[-2,0)上单调递减,在(0,2)上单调递增
∴当x=0时,函数有最小值f(0)=2
∵f(2)=6,f(-2)=22
当x=-2时,函数有最大值22
故选A

练习册系列答案
相关题目
 .
. ,
,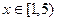 的值域为
的值域为  (
(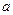 >0且
>0且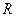 ,则实数
,则实数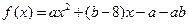 ,当
,当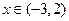 时,
时,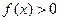 ;当
;当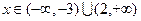 时,
时, .(1)
.(1) 为何值时
为何值时 的解集为
的解集为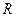 ;(2)求
;(2)求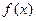 在
在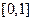 内的值域.
内的值域.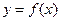 的定义域是
的定义域是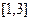 ,则函数
,则函数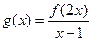 的定义域是
的定义域是