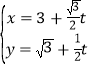题目内容
【题目】已知椭圆
（a＞b＞0）的离心率为
，过椭圆的左、右焦点
分别作倾斜角为
的直线
，
分别交椭圆于A，B和C，D两点，当
时，直线AB与CD之间的距离为
.
（1）求椭圆的标准方程；
（2）若AB不与x轴重合，点P在椭圆上，且满足
（t＞0）.若
，求直线AB的方程.
【答案】（1）
；（2）
.
【解析】
（1）当
时，直线AB与CD之间的距离为
，得
，所以
，由椭圆C的离心率为
，
，可求椭圆方程.（2）先验证直线
的斜率不存在时，不满足题意，当直线的斜率存在时，设方程为
，联立直线和椭圆方程，设
，由
，把
代入椭圆方程得
，即可求AB方程.
解：（1）设
，由
之间的距离为，得，所以，
由椭圆C的离心率为，得
，所以，
，
所以椭圆C的标准方程为.
（2）若直线的斜率不存在，则易得
，
，得
，显然点
不在椭圆上，舍去
因此设直线的方程为，设，
将直线的方程与椭圆
的方程联立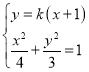
，整理得
，
因为
，所以
，
则由，
得
将P点坐标代入椭圆C的方程，得
;
将带入等式
得，
因此所求直线AB的方程为
练习册系列答案
阅读快车系列答案
相关题目
