Question

【题目】如图，在三棱锥A﹣BCD中，AB=AD，BD⊥CD，点E、F分别是棱BC、BD的中点．

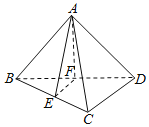
（1）求证：EF∥平面ACD；

（2）求证：AE⊥BD．

Answer 1

【答案】（1）证明见解析（2）证明见解析

【解析】

（1）证明EF∥CD，然后利用直线与平面平行的判断定理证明EF∥平面ACD；

（2）证明BD⊥平面AEF，然后说明AE⊥BD．

（1）因为点E、F分别是棱BC、BD的中点，

所以EF是△BCD的中位线，

所以EF∥CD，又因为EF平面ACD，CD平面ACD，

EF∥平面ACD．

（2）由（1）得，EF∥CD，又因为BD⊥CD，所以EF⊥BD，

因为AB=AD，点F是棱BD的中点，所以AF⊥BD，

又因为EF∩AF=F，所以BD⊥平面AEF，

又因为AE平面AEF，

所以AE⊥BD．