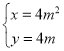题目内容
【题目】在直角坐标系![]() 中,以坐标原点
中,以坐标原点![]() 务极点,
务极点,![]() 轴正半轴为极轴建立极坐标系,曲线
轴正半轴为极轴建立极坐标系,曲线![]() ,
,![]()
(1)求曲线![]() ,
,![]() 的直角坐标方程;
的直角坐标方程;
(2)曲线![]() 和
和![]() 的交点为
的交点为![]() ,
,![]() ,求以
,求以![]() 为直径的圆与
为直径的圆与![]() 轴的交点坐标.
轴的交点坐标.
【答案】(1) ![]() :
: ![]() ;
;![]() :
:![]() (2)
(2) ![]() 点坐标为
点坐标为![]() 或
或![]()
【解析】
(Ⅰ)根据极坐标与直角坐标的互化公式,即可求解曲线![]() 的直角坐标方程;
的直角坐标方程;
(Ⅱ)先求出MN的中点坐标,|MN|的长,可求得圆的方程,再令x=0,即可求解.
(Ⅰ)由sin(θ+![]() )=
)=![]() ,得ρ(sinθcos
,得ρ(sinθcos![]() +cosθsin
+cosθsin![]() )=
)=![]() ,
,
将![]() 代入上得x+y=1,即C1的直角坐标方程为x+y+1=0,
代入上得x+y=1,即C1的直角坐标方程为x+y+1=0,
同理由ρ2=![]() ,可得3x2-y2=1,∴C2的直角坐标方程为3x2-y2=1.
,可得3x2-y2=1,∴C2的直角坐标方程为3x2-y2=1.
(Ⅱ)∵PM⊥PN,先求以MN为直径的圆,设Mx1,y1),N(x2,y2),
由![]() 得3x2-(1-x)2=1,即x2+x-1=0,
得3x2-(1-x)2=1,即x2+x-1=0,
∴![]() ,则MN的中点坐标为(-
,则MN的中点坐标为(-![]() ,
,![]() ),
),
由弦长公式,可得|MN|=![]() |x1-x2|=
|x1-x2|=![]()
![]() =
=![]() .
.
∴以MN为直径的圆:(x+![]() )2+(y-
)2+(y-![]() )2=(
)2=(![]() )2,
)2,
令x=0,得![]() +(y-
+(y-![]() )2=
)2=![]() ,即(y-
,即(y-![]() )2=
)2=![]() ,∴y=0或y=3,
,∴y=0或y=3,
∴所求P点的坐标为(0,0)或(0,3).

练习册系列答案
相关题目