题目内容
【题目】选修4-4:坐标系与参数方程
在平面直角坐标系![]() 中,以
中,以![]() 为极点,
为极点, ![]() 轴的正半轴为极轴的极坐标系中,直线
轴的正半轴为极轴的极坐标系中,直线![]() 的极坐标方程为
的极坐标方程为![]() ,曲线
,曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数).
为参数).
(Ⅰ)写出直线![]() 与曲线
与曲线![]() 的直角坐标方程:
的直角坐标方程:
(Ⅱ)过点![]() 平行于直线
平行于直线![]() 的直线与曲线
的直线与曲线![]() 交于
交于![]() 、
、![]() 两点,若
两点,若![]() ,求点
,求点![]() 轨迹的直角坐标方程.
轨迹的直角坐标方程.
【答案】(1)![]() ,
, ![]() .(2)
.(2)![]() (夹在两直线
(夹在两直线![]() 之间的两段圆弧)
之间的两段圆弧)
【解析】试题分析:(1)根据题意,由极坐标方程的定义可得直线l的方程,对于曲线C的参数方程,消去参数计算即可得答案;(2)设点M(x0.y0)及过点M的直线,结合题意直线L1与曲线C相交可得关于t的二次方程,又由题意可得![]() ,将其变形可得答案.
,将其变形可得答案.
解析:
(Ⅰ)直线![]() 的极坐标方程为
的极坐标方程为![]() ,所以直线斜率为1,直线
,所以直线斜率为1,直线![]() .
.
曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),消去参数
为参数),消去参数![]() ,可得曲线
,可得曲线![]() .
.
(Ⅱ)设点![]() 及过点
及过点![]() 的直线为
的直线为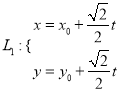 (
(![]() 为参数).
为参数).
由直线![]() 与曲线
与曲线![]() 相交可得:
相交可得:
![]() .
.
因为![]() ,所以
,所以![]() ,即:
,即: ![]() .
.
![]() ,
,
由![]() .
.
故点![]() 的轨迹的直角坐标方程为:
的轨迹的直角坐标方程为: ![]() (夹在两直线
(夹在两直线![]() 之间的两段圆弧).
之间的两段圆弧).

 高效智能课时作业系列答案
高效智能课时作业系列答案 捷径训练检测卷系列答案
捷径训练检测卷系列答案【题目】海关对同时从![]() 三个不同地区进口的某种商品进行抽样检测,从各地区进口此种商品的数量(单位:件)如表所示,工作人员用分层抽样的方法从这些商品中共抽取7件样品进行检测.
三个不同地区进口的某种商品进行抽样检测,从各地区进口此种商品的数量(单位:件)如表所示,工作人员用分层抽样的方法从这些商品中共抽取7件样品进行检测.
地区 |
|
|
|
数量 | 200 | 50 | 100 |
(1)求这7件样品中来自![]() 各地区样品的数量;
各地区样品的数量;
(2)若在这7件样品中随机抽取2件送往甲机构进行进一步检测,求这2件商品来自相同地区的概率.
【题目】某葡萄基地的种植专家发现,葡萄每株的收获量![]() (单位:
(单位: ![]() )和与它“相近”葡萄的株数
)和与它“相近”葡萄的株数![]() 具有线性相关关系(所谓两株作物“相近”是指它们的直线距离不超过
具有线性相关关系(所谓两株作物“相近”是指它们的直线距离不超过![]() ),并分别记录了相近葡萄的株数为1,2,3,4,5,6,7时,该葡萄每株收获量的相关数据如下:
),并分别记录了相近葡萄的株数为1,2,3,4,5,6,7时,该葡萄每株收获量的相关数据如下:
| 1 | 2 | 3 | 5 | 6 | 7 |
| 15 | 13 | 12 | 10 | 9 | 7 |
(1)求该葡萄每株的收获量![]() 关于它“相近”葡萄的株数
关于它“相近”葡萄的株数![]() 的线性回归方程及
的线性回归方程及![]() 的方差
的方差![]() ;
;
(2)某葡萄专业种植户种植了1000株葡萄,每株“相近”的葡萄株数按2株计算,当年的葡萄价格按10元/ ![]() 投入市场,利用上述回归方程估算该专业户的经济收入为多少万元;(精确到0.01)
投入市场,利用上述回归方程估算该专业户的经济收入为多少万元;(精确到0.01)
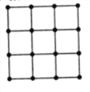
(3)该葡萄基地在如图所示的正方形地块的每个格点(指纵、横直线的交叉点)处都种了一株葡萄,其中每个小正方形的面积都为![]() ,现在所种葡萄中随机选取一株,求它的收获量的分布列与数学期望.(注:每株收获量以线性回归方程计算所得数据四舍五入后取的整数为依据)
,现在所种葡萄中随机选取一株,求它的收获量的分布列与数学期望.(注:每株收获量以线性回归方程计算所得数据四舍五入后取的整数为依据)