题目内容
【题目】某葡萄基地的种植专家发现,葡萄每株的收获量![]() (单位:
(单位: ![]() )和与它“相近”葡萄的株数
)和与它“相近”葡萄的株数![]() 具有线性相关关系(所谓两株作物“相近”是指它们的直线距离不超过
具有线性相关关系(所谓两株作物“相近”是指它们的直线距离不超过![]() ),并分别记录了相近葡萄的株数为1,2,3,4,5,6,7时,该葡萄每株收获量的相关数据如下:
),并分别记录了相近葡萄的株数为1,2,3,4,5,6,7时,该葡萄每株收获量的相关数据如下:
| 1 | 2 | 3 | 5 | 6 | 7 |
| 15 | 13 | 12 | 10 | 9 | 7 |
(1)求该葡萄每株的收获量![]() 关于它“相近”葡萄的株数
关于它“相近”葡萄的株数![]() 的线性回归方程及
的线性回归方程及![]() 的方差
的方差![]() ;
;
(2)某葡萄专业种植户种植了1000株葡萄,每株“相近”的葡萄株数按2株计算,当年的葡萄价格按10元/ ![]() 投入市场,利用上述回归方程估算该专业户的经济收入为多少万元;(精确到0.01)
投入市场,利用上述回归方程估算该专业户的经济收入为多少万元;(精确到0.01)
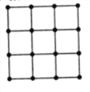
(3)该葡萄基地在如图所示的正方形地块的每个格点(指纵、横直线的交叉点)处都种了一株葡萄,其中每个小正方形的面积都为![]() ,现在所种葡萄中随机选取一株,求它的收获量的分布列与数学期望.(注:每株收获量以线性回归方程计算所得数据四舍五入后取的整数为依据)
,现在所种葡萄中随机选取一株,求它的收获量的分布列与数学期望.(注:每株收获量以线性回归方程计算所得数据四舍五入后取的整数为依据)
【答案】(1)线性回归方程为![]() ,方差为7;(2)总收入为
,方差为7;(2)总收入为![]() ;(3)见解析.
;(3)见解析.
【解析】【试题分析】(1)利用回归直线方程的公式,计算![]() 的值,由此求得回归直线方程.利用样本方差的公式计算得方差.(2)将
的值,由此求得回归直线方程.利用样本方差的公式计算得方差.(2)将![]() 代入回归直线方程,求得对应预报变量的值,进而求得总收入.(3)
代入回归直线方程,求得对应预报变量的值,进而求得总收入.(3)![]() 可能的取值为
可能的取值为![]() ,利用回归直线方程,求出对应
,利用回归直线方程,求出对应![]() 的值为
的值为![]() ,求得对应概率后列表得到分布列并计算出期望值.
,求得对应概率后列表得到分布列并计算出期望值.
【试题解析】
(1)由题意,可知![]() ,
,
![]() .
.
![]()
![]()
![]() ,
,
![]()
![]() ,
,
所以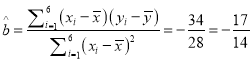 ,
,
所以![]() ,
,
故该葡萄每株收获量![]() 关于它“相近”葡萄的株数
关于它“相近”葡萄的株数![]() 的线性回归方程为
的线性回归方程为![]() .
.
![]() 的方差为
的方差为
![]()
![]() .
.
(2)由![]() ,可知当
,可知当![]() 时,
时, ![]() ,
,
因此总收入为![]() (万元).
(万元).
(3)由题知, ![]() .
.
由(1)(2),知当![]() 时,
时, ![]() ,所以
,所以![]() ;
;
当![]() 时,
时, ![]() ,所以
,所以![]() ;
;
当![]() 时,
时, ![]() ,
,
即![]() 时,与之相对应的
时,与之相对应的![]() 的值分别为13,12,11,
的值分别为13,12,11,
又![]() ,
,
![]() ,
,
![]() ,
,
所以在所种葡萄中随机选取一株,它的收获量![]() 的分布列为
的分布列为
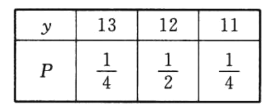
![]() .
.

【题目】某种新产品投放市场的100天中,前40天价格呈直线上升,而后60天其价格呈直线下降,现统计出其中4天的价格如下表:
时间 | 第4天 | 第32天 | 第60天 | 第90天 |
价格(千元) | 23 | 30 | 22 | 7 |
(1)写出价格![]() 关于时间
关于时间![]() 的函数关系式;(
的函数关系式;(![]() 表示投放市场的第
表示投放市场的第![]() 天);
天);
(2)销售量![]() 与时间
与时间![]() 的函数关系:
的函数关系:![]() ,则该产品投放市场第几天销售额最高?最高为多少千元?
,则该产品投放市场第几天销售额最高?最高为多少千元?