题目内容
【题目】如果既约分数![]() 满足:
满足:![]() (
(![]() 、
、![]() 为正整数),则称
为正整数),则称![]() 为“牛分数”.现将所有的牛分数按递增顺序排成一个数列
为“牛分数”.现将所有的牛分数按递增顺序排成一个数列![]() ,称为“牛数列”.证明:对于牛数列中的任两个相邻项
,称为“牛数列”.证明:对于牛数列中的任两个相邻项![]() 、
、![]() ,都满足
,都满足![]() .
.
【答案】见解析
【解析】
对任一正整数![]() ,将牛数列中分母不大于
,将牛数列中分母不大于![]() 的子数列记为
的子数列记为![]() .
.
当![]() 时,数列
时,数列![]() 显然满足条件.
显然满足条件.
对![]() 进行归纳.
进行归纳.
据数列![]() 知,当
知,当![]() 时结论成立.
时结论成立.
设结论对于![]() 成立,考虑数列
成立,考虑数列![]() .
.
注意到![]() ,而
,而![]() 中的分数
中的分数![]() 满足:分母
满足:分母![]() ,
,![]() .
.
设![]() 、
、![]() 是
是![]() 中的一对相邻分数.
中的一对相邻分数.
如果它们在![]() 中也相邻,则显然满足条件;
中也相邻,则显然满足条件;
如果它们在![]() 中不相邻,即有
中不相邻,即有![]() 中的分数
中的分数![]() 插入它们之间(
插入它们之间(![]() ,
,![]() ),即
),即![]() (插入的分数中总有一个与
(插入的分数中总有一个与![]() 或
或![]() 相邻,不妨设
相邻,不妨设![]() 与
与![]() 相邻).
相邻).
于是,![]() . ①
. ①
所以,![]() .
.
又易知,分数![]() 也介于
也介于![]() 与
与![]() 之间(这是由于
之间(这是由于![]() ,
,![]() ).
).
注意到![]() ,知
,知![]() 与
与![]() 互质,即
互质,即![]() 为既约分数.
为既约分数.
若![]() ,由
,由![]() 及
及![]() ,相乘得
,相乘得![]() .
.
由![]() ,得
,得![]() .
.
又![]() ,且
,且![]() 、
、![]() 在
在![]() 中相邻,则
中相邻,则![]() ,且式①中等号成立.
,且式①中等号成立.
故![]() .
.
从而,![]() ,这与
,这与![]() 矛盾.
矛盾.
因此,![]() .
.
若分数![]() ,则
,则![]() . ②
. ②
若![]() 、
、![]() 、
、![]() 是
是![]() 中的相邻项,那么,对于前一对分数而言有
中的相邻项,那么,对于前一对分数而言有![]() ;
;
而对于后一对分数而言有![]() .
.
因此,插入![]() 后的分数列符合条件.
后的分数列符合条件.
又由式②知,式①等号成立.于是,![]() 以及
以及![]() .
.
由![]() ,得
,得![]() . ③
. ③
因此,![]() .
.
又![]() 是
是![]() 中能够插入
中能够插入![]() 中的一对相邻分数
中的一对相邻分数![]() 、
、![]() 之间的唯一分数,即在由数列
之间的唯一分数,即在由数列![]() 过渡到数列
过渡到数列![]() 时,不论相邻分数间是否插入了新的分数,所得数列
时,不论相邻分数间是否插入了新的分数,所得数列![]() 都满足条件.
都满足条件.
因此,对于每个正整数![]() ,结论成立.特别是数列
,结论成立.特别是数列![]() 满足条件,故本题得证.
满足条件,故本题得证.

【题目】近年来,我国工业经济发展迅速,工业增加值连年攀升,某研究机构统计了近十年(从2008年到2017年)的工业增加值(万亿元),如下表:
年份 | 2008 | 2009 | 2010 | 2011 | 2012 | 2013 | 2014 | 2015 | 2016 | 2017 |
年份序号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
工业增加值 | 13.2 | 13.8 | 16.5 | 19.5 | 20.9 | 22.2 | 23.4 | 23.7 | 24.8 | 28 |
依据表格数据,得到下面的散点图及一些统计量的值.
|
|
|
|
|
5.5 | 20.6 | 82.5 | 211.52 | 129.6 |
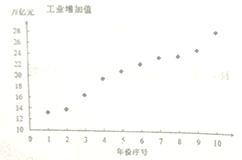
(1)根据散点图和表中数据,此研究机构对工业增加值![]() (万亿元)与年份序号
(万亿元)与年份序号![]() 的回归方程类型进行了拟合实验,研究人员甲采用函数
的回归方程类型进行了拟合实验,研究人员甲采用函数![]() ,其拟合指数
,其拟合指数![]() ;研究人员乙采用函数
;研究人员乙采用函数![]() ,其拟合指数
,其拟合指数![]() ;研究人员丙采用线性函数
;研究人员丙采用线性函数![]() ,请计算其拟合指数,并用数据说明哪位研究人员的函数类型拟合效果最好.(注:相关系数
,请计算其拟合指数,并用数据说明哪位研究人员的函数类型拟合效果最好.(注:相关系数![]() 与拟合指数
与拟合指数![]() 满足关系
满足关系![]() ).
).
(2)根据(1)的判断结果及统计值,建立![]() 关于
关于![]() 的回归方程(系数精确到0.01);
的回归方程(系数精确到0.01);
(3)预测到哪一年的工业增加值能突破30万亿元大关.
附:样本
![]() 的相关系数
的相关系数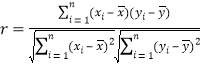 ,
,
![]() ,
, ,
,![]() .
.
【题目】“难度系数”反映试题的难易程度,难度系数越大,题目得分率越高,难度也就越小.“难度系数”的计算公式为![]() ,其中,
,其中,![]() 为难度系数,
为难度系数,![]() 为样本平均失分,
为样本平均失分,![]() 为试卷总分(一般为100分或150分).某校高三年级的李老师命制了某专题共5套测试卷(每套总分150分),用于对该校高三年级480名学生进行每周测试.测试前根据自己对学生的了解,预估了每套试卷的难度系数,如下表所示:
为试卷总分(一般为100分或150分).某校高三年级的李老师命制了某专题共5套测试卷(每套总分150分),用于对该校高三年级480名学生进行每周测试.测试前根据自己对学生的了解,预估了每套试卷的难度系数,如下表所示:
试卷序号 | 1 | 2 | 3 | 4 | 5 |
考前预估难度系数 | 0.7 | 0.64 | 0.6 | 0.6 | 0.55 |
测试后,随机抽取了50名学生的数据进行统计,结果如下:
试卷序号 | 1 | 2 | 3 | 4 | 5 |
实测平均分 | 102 | 99 | 93 | 93 | 87 |
(1)根据试卷2的难度系数估计这480名学生第2套试卷的平均分;
(2)从抽样的50名学生的5套试卷中随机抽取2套试卷,记这2套试卷中平均分超过96分的套数为![]() ,求
,求![]() 的分布列和数学期望;
的分布列和数学期望;
(3)试卷的预估难度系数和实测难度系数之间会有偏差.设![]() 为第
为第![]() 套试卷的实测难度系数,并定义统计量
套试卷的实测难度系数,并定义统计量![]() ,若
,若![]() ,则认为本专题的5套试卷测试的难度系数预估合理,否则认为不合理.试检验本专题的5套试卷对难度系数的预估是否合理.
,则认为本专题的5套试卷测试的难度系数预估合理,否则认为不合理.试检验本专题的5套试卷对难度系数的预估是否合理.