题目内容
【题目】已知椭圆
的离心率为
，
分别为
的左、右顶点，
是上异于的动点，
面积的最大值为2.
（1）求椭圆的方程；
（2）证明：直线
与直线
的斜率乘积为定值；
（3）设直线，分别交直线
于
两点，以
为直径作圆，当圆的面积最小时，求该圆的方程.
【答案】（1）
（2）详见解析（3）
【解析】
（1）依题意有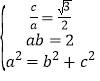
，解出方程即可；（2）由（1）知
，
，
，
，再利用点在曲线上得到结果;(3)根据第二问设出直线PA和PB，解出点M，N的点坐标，进而得到圆心Q的坐标，可以写出圆的方程，由均值不等式得到最值.
（1）依题意有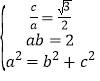，解得
，
，
故所求椭圆方程为.
（2）由（1）知，，
设，则
，
，
即直线
与直线
的斜率乘积为定值
.
（3）设直线：
，则直线：
，
令
得
，
，
∴
的中点为
，
，
于是以为直径的圆的方程为
，
，当且仅当
即
时等号成立.
此时圆的方程为
.
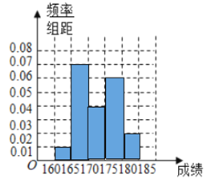
计算高手系列答案
【题目】某大型电器企业，为了解组装车间职工的生活情况，从中随机抽取了
名职工进行测试，得到频数分布表如下：
日组装个数 |
|
|
|
|
|
|
人数 | 6 | 12 | 34 | 30 | 10 | 8 |
（1）现从参与测试的日组装个数少于
的职工中任意选取
人，求至少有
人日组装个数少于
的概率；
（2）由频数分布表可以认为，此次测试得到的日组装个数
服从正态分布
，
近似为这人得分的平均值（同一组数据用该组区间的中点值作为代表）.
（
名职工，求日组装个数超过
的职工人数；
（ii）为鼓励职工提高技能，企业决定对日组装个数超过
的职工日工资增加
元，若在组装车间所有职工中任意选取人，求这三人增加的日工资总额的期望.
附：若随机变量
服从正态分布
，则
，
，
.
【题目】近年来，共享单车在我国各城市迅猛发展，为人们的出行提供了便利，但也给城市的交通管理带来了一些困难，为掌握共享单车在
省的发展情况，某调查机构从该省抽取了5个城市，并统计了共享单车的
指标
和
指标
，数据如下表所示：
城市1 | 城市2 | 城市3 | 城市4 | 城市5 | |
| 2 | 4 | 5 | 6 | 8 |
| 3 | 4 | 4 | 4 | 5 |
（1）试求与间的相关系数
，并说明与是否具有较强的线性相关关系（若
，则认为与具有较强的线性相关关系，否则认为没有较强的线性相关关系）.
（2）建立关于的回归方程，并预测当指标为7时，指标的估计值.
（3）若某城市的共享单车指标在区间
的右侧，则认为该城市共享单车数量过多，对城市的交通管理有较大的影响交通管理部门将进行治理，直至指标在区间内现已知省某城市共享单车的指标为13，则该城市的交通管理部门是否需要进行治理？试说明理由.
参考公式：回归直线
中斜率和截距的最小二乘估计分别为
，，
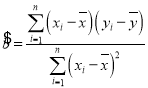相关系数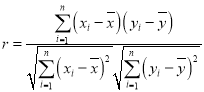
参考数据：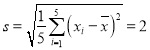
，
，
.