题目内容
【题目】在三棱锥![]() 中,平面
中,平面![]() 平面
平面![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.
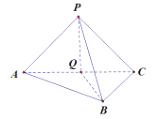
(1)证明:![]() ;
;
(2)求直线![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
【答案】(1)详见解析(2)![]()
【解析】
(1)利用面面垂直,可证![]() 平面
平面![]() ,从而有
,从而有![]() ,再利用勾股定理证明
,再利用勾股定理证明![]() ,可证
,可证![]() 平面
平面![]() ,证得结论.
,证得结论.
(2)先证得平面![]() 平面
平面![]() ,过点
,过点![]() 作
作![]() 于点
于点![]() ,有
,有![]() 平面
平面![]() ,可证明
,可证明![]() 是
是![]() 与平面
与平面![]() 所成的角,在△ABC中,求得
所成的角,在△ABC中,求得![]() ,可得
,可得![]() ,由等面积法知
,由等面积法知![]() ,即可求解直线
,即可求解直线![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
(1)由题意平面![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,平面
,平面![]() 平面
平面![]() =AC,
=AC,
又![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() 平面
平面![]() ,从而有
,从而有![]() ,
,
又由勾股定理得![]() ,
,![]() ,
,
∴![]() 平面
平面![]() ,即
,即![]() ;
;
(2)设![]() ,则
,则![]() ,
,
在![]() 中,
中,![]() ,即
,即![]() .
.
故![]() ,
,![]() ,
,
过![]() 作
作![]() 于点
于点![]() ,连接
,连接![]() ,过点
,过点![]() 作
作![]() 于点
于点![]() ,
,
连接![]() ,因为
,因为![]() 且
且![]() ,
,
故![]() 平面
平面![]() ,
,
又因为![]() 平面
平面![]() ,所以平面
,所以平面![]() 平面
平面![]() ,
,
进而有![]() 平面
平面![]() ,
,
故![]() 是
是![]() 与平面
与平面![]() 所成的角,
所成的角,
在![]() 中,有
中,有![]() ,得
,得![]() ,
,
故![]() ,
,![]() ,
,
由等面积法知![]() ,
,
所以![]() ,
,
故直线![]() 与平面
与平面![]() 所成角的正弦值为
所成角的正弦值为![]() .
.

 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案【题目】如图是某公司一种产品的日销售量![]() (单位:百件)关于日最高气温
(单位:百件)关于日最高气温![]() (单位:
(单位:![]() )的散点图.
)的散点图.

数据:
| 13 | 15 | 19 | 20 | 21 |
| 26 | 28 | 30 | 18 | 36 |
(1)请剔除一组数据,使得剩余数据的线性相关性最强,并用剩余数据求日销售量![]() 关于日最高气温
关于日最高气温![]() 的线性回归方程
的线性回归方程![]() ;
;
(2)根据现行《重庆市防暑降温措施管理办法》.若气温超过36度,职工可享受高温补贴.已知某日该产品的销售量为53.1,请用(1)中求出的线性回归方程判断该公司员工当天是否可享受高温补贴?
附: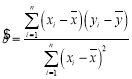 ,
,![]() .
.
【题目】某大型电器企业,为了解组装车间职工的生活情况,从中随机抽取了![]() 名职工进行测试,得到频数分布表如下:
名职工进行测试,得到频数分布表如下:
日组装个数 |
|
|
|
|
|
|
人数 | 6 | 12 | 34 | 30 | 10 | 8 |
(1)现从参与测试的日组装个数少于![]() 的职工中任意选取
的职工中任意选取![]() 人,求至少有
人,求至少有![]() 人日组装个数少于
人日组装个数少于![]() 的概率;
的概率;
(2)由频数分布表可以认为,此次测试得到的日组装个数![]() 服从正态分布
服从正态分布![]() ,
,![]() 近似为这
近似为这![]() 人得分的平均值(同一组数据用该组区间的中点值作为代表).
人得分的平均值(同一组数据用该组区间的中点值作为代表).
(![]() 名职工,求日组装个数超过
名职工,求日组装个数超过![]() 的职工人数;
的职工人数;
(ii)为鼓励职工提高技能,企业决定对日组装个数超过![]() 的职工日工资增加
的职工日工资增加![]() 元,若在组装车间所有职工中任意选取
元,若在组装车间所有职工中任意选取![]() 人,求这三人增加的日工资总额的期望.
人,求这三人增加的日工资总额的期望.
附:若随机变量![]() 服从正态分布
服从正态分布![]() ,则
,则![]() ,
,![]() ,
,![]() .
.