题目内容
【题目】求所有的实数组(a、b、c),使得对任何整数n,都有![]() .其中,
.其中,![]() 表示不超过实数x的最大整数.
表示不超过实数x的最大整数.
【答案】见解析
【解析】
首先证明:“使对任何整数n,都有![]() ”等价于“a、b中至少有一个为整数,且c=a+b”.
”等价于“a、b中至少有一个为整数,且c=a+b”.
一方面,若a、b中至少有一个为整数,且c=a+b,则不妨设a为整数.那么,对任何整数n,na为整数.所以,![]() .
.
于是,![]()
![]() .
.
另一方面,若对任何整数n,都有![]() .则分别取n=1、-1,
.则分别取n=1、-1,
得![]() ,
,![]()
两式相加得![]() .
.
又对任何实数x,![]()
![]()
于是,如果a、b都不是整数,则![]()
故![]() ,矛盾.
,矛盾.
所以,a、b中至少有一个为整数.
不妨设a为整数,那么,对任何整数n,na为整数,于是,![]() .
.
则对任何整数n,![]() .
.
即![]() .
.
故![]()
而![]()
于是,![]() .
.
综上,所求的实数组![]() ,
,![]() ,
,![]()
其中,m、n为任意整数,t为任意实数.

练习册系列答案
相关题目
【题目】如图是某公司一种产品的日销售量![]() (单位:百件)关于日最高气温
(单位:百件)关于日最高气温![]() (单位:
(单位:![]() )的散点图.
)的散点图.

数据:
| 13 | 15 | 19 | 20 | 21 |
| 26 | 28 | 30 | 18 | 36 |
(1)请剔除一组数据,使得剩余数据的线性相关性最强,并用剩余数据求日销售量![]() 关于日最高气温
关于日最高气温![]() 的线性回归方程
的线性回归方程![]() ;
;
(2)根据现行《重庆市防暑降温措施管理办法》.若气温超过36度,职工可享受高温补贴.已知某日该产品的销售量为53.1,请用(1)中求出的线性回归方程判断该公司员工当天是否可享受高温补贴?
附: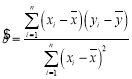 ,
,![]() .
.

