题目内容
15.已知函数f(x)=$\left\{\begin{array}{l}{x+\frac{1}{x},x>0}\\{{x}^{3}+3,x≤0}\end{array}\right.$,则关于x的方程f(2x2+x)=k(2<k≤3)的根的个数不可能为( )| A. | 6 | B. | 5 | C. | 4 | D. | 3 |
分析 画出函数f(x)=$\left\{\begin{array}{l}{x+\frac{1}{x},x>0}\\{{x}^{3}+3,x≤0}\end{array}\right.$ 的图象,令t=2x2+x,分类讨论求得y=a与y=f(t)的图象的交点个数,
可得结论.
解答  解:画出函数f(x)=$\left\{\begin{array}{l}{x+\frac{1}{x},x>0}\\{{x}^{3}+3,x≤0}\end{array}\right.$ 的图象如右图,
解:画出函数f(x)=$\left\{\begin{array}{l}{x+\frac{1}{x},x>0}\\{{x}^{3}+3,x≤0}\end{array}\right.$ 的图象如右图,
令t=2x2+x,
当2<a≤3时,y=a与y=f(t)的图象有三个交点,
三个交点的横坐标记为t1,t2,t3且t1≤0<t2<t3,
当2x2+x=t2时,该方程有两解,2x2+x=t3时,
该方程也有两解.
当2x2+x=t1时,该方程有0个解或1个解或2个解,
∴当2<a≤3时,方程f(2x2+x)=a的根的个数可能
为4个,5个,6个.
当a>3时,y=a与y=f(t)的图象有两个交点,
两个交点的横坐标记为t4,t5且0<t4<t5,
当2x2+x=t4时,该方程有两解,2x2+x=t5时,该方程也有两解,
∴当a>3时,方程f(2x2+x)=a的根的个数为4个.
综上所述:方程f(2x2+x)=a(a>2)的根的个数可能为4个,5个,6个,
不可能是3个,
故选:D.
点评 本题主要考查方程根的存在性以及个数判断,体现了转化、分类讨论的数学思想,属于中档题.

练习册系列答案
相关题目
10.如图,点B是⊙O的半径OA的中点,且CD⊥OA于B,则tan∠CPD的值为( )?
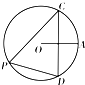

| A. | $\frac{1}{2}$ | B. | $\frac{\sqrt{3}}{3}$ | C. | $\frac{\sqrt{3}}{2}$ | D. | $\sqrt{3}$ |
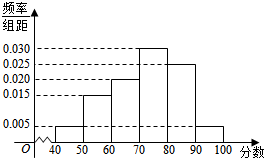 某校对参加高校自主招生测试的学生进行模拟训练,从中抽出N名学生,其数学成绩的频率分布直方图如图所示.已知成绩在区间[90,100]内的学生人数为2人.
某校对参加高校自主招生测试的学生进行模拟训练,从中抽出N名学生,其数学成绩的频率分布直方图如图所示.已知成绩在区间[90,100]内的学生人数为2人.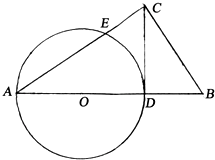 Rt△ABC中,∠C=90°,CD⊥AB,AD为圆O的直径,圆O与AC交于E,求证:$\frac{AE}{CE}$=$\frac{A{C}^{2}}{B{C}^{2}}$.
Rt△ABC中,∠C=90°,CD⊥AB,AD为圆O的直径,圆O与AC交于E,求证:$\frac{AE}{CE}$=$\frac{A{C}^{2}}{B{C}^{2}}$.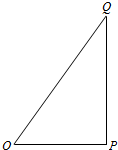 如图,O,P,Q三地有直道相通,OP=3千米,PQ=4千米,OQ=5千米,现甲、乙两警员同时从O地出发匀速前往Q地,经过t小时,他们之间的距离为f(t)(单位:千米).甲的路线是OQ,速度为5千米/小时,乙的路线是OPQ,速度为8千米/小时,乙到达Q地后在原地等待.设t=t1时乙到达P地,t=t2时乙到达Q地.
如图,O,P,Q三地有直道相通,OP=3千米,PQ=4千米,OQ=5千米,现甲、乙两警员同时从O地出发匀速前往Q地,经过t小时,他们之间的距离为f(t)(单位:千米).甲的路线是OQ,速度为5千米/小时,乙的路线是OPQ,速度为8千米/小时,乙到达Q地后在原地等待.设t=t1时乙到达P地,t=t2时乙到达Q地.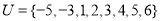 ,集合
,集合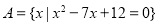 ,集合
,集合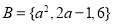 .若
.若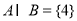 ,且
,且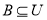 ,则
,则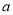 等于( )
等于( )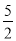 B.
B.