题目内容
8.已知a,b均为正整数,圆x2+y2-2ax+a2(1-b)=0与圆x2+y2-2y+1-a2b=0外切,则ab的最小值为$\frac{1}{2}$.分析 通过圆的位置关系,推出ab关系,然后利用基本不等式求出最值即可.
解答 解:圆x2+y2-2ax+a2(1-b)=0的圆心(a,0),半径:$a\sqrt{b}$;
圆x2+y2-2y+1-a2b=0的圆心(0,1),半径:$a\sqrt{b}$;
两个圆外切,可得a2+1=4a2b,
可得ab=$\frac{{a}^{2}+1}{4a}$=$\frac{a}{4}+\frac{1}{4a}$≥$2\sqrt{\frac{a}{4}•\frac{1}{4a}}$=$\frac{1}{2}$,当且仅当a=1时等号成立.
故答案为:$\frac{1}{2}$.
点评 本题考查圆的位置关系的应用,基本不等式的应用,考查计算能力.

练习册系列答案
相关题目
13.已知数列{an}满足a1=3,且an+1=4an+3(n∈N*),则数列{an}的通项公式为( )
| A. | 22n-1+1 | B. | 22n-1-1 | C. | 22n+1 | D. | 22n-1 |
16.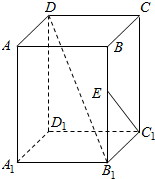 在四棱柱ABCD-A1B1C1D1中,AA1⊥平面A1B1C1D1,底面A1B1C1D1是边长为a的正方形,侧棱AA1的长为b,E为侧棱BB1上的动点(包括端点),则( )
在四棱柱ABCD-A1B1C1D1中,AA1⊥平面A1B1C1D1,底面A1B1C1D1是边长为a的正方形,侧棱AA1的长为b,E为侧棱BB1上的动点(包括端点),则( )
 在四棱柱ABCD-A1B1C1D1中,AA1⊥平面A1B1C1D1,底面A1B1C1D1是边长为a的正方形,侧棱AA1的长为b,E为侧棱BB1上的动点(包括端点),则( )
在四棱柱ABCD-A1B1C1D1中,AA1⊥平面A1B1C1D1,底面A1B1C1D1是边长为a的正方形,侧棱AA1的长为b,E为侧棱BB1上的动点(包括端点),则( )| A. | 对任意的a,b,存在点E,使得B1D⊥EC1 | |
| B. | 当且仅当a=b时,存在点E,使得B1D⊥EC1 | |
| C. | 当且仅当a≤b时,存在点E,使得B1D⊥EC1 | |
| D. | 当且仅当a≥b时,存在点E,使得B1D⊥EC1 |
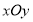 中,动点
中,动点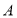 的坐标为
的坐标为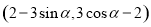 ,其中
,其中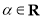 .在极坐标系(以原点
.在极坐标系(以原点 为极点,以
为极点,以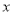 轴非负半轴为极轴)中,直线
轴非负半轴为极轴)中,直线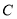 的方程为
的方程为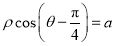 .
.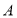 的轨迹的形状;
的轨迹的形状;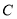 与动点
与动点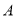 的轨迹有且仅有一个公共点,求实数
的轨迹有且仅有一个公共点,求实数 的值.
的值.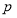 :若
:若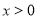 ,则函数
,则函数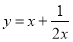 的最小值为
的最小值为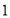 ;命题
;命题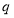 :若
:若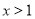 ,则
,则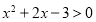 .则
.则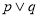 B.
B.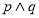
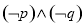 D.
D.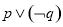
 如图,已知四边形ABCD内接于半径为3的圆,且AB是圆的直径.经过点D的圆的切线与BA的延长线交于点M.∠BMD的平分线分别交AD,BD于点E,FAC,BD交于点P.
如图,已知四边形ABCD内接于半径为3的圆,且AB是圆的直径.经过点D的圆的切线与BA的延长线交于点M.∠BMD的平分线分别交AD,BD于点E,FAC,BD交于点P.