题目内容
10.如图,点B是⊙O的半径OA的中点,且CD⊥OA于B,则tan∠CPD的值为( )?
| A. | $\frac{1}{2}$ | B. | $\frac{\sqrt{3}}{3}$ | C. | $\frac{\sqrt{3}}{2}$ | D. | $\sqrt{3}$ |
分析 连接OC、OD,由垂径定理和圆周角定理可得∠COB=∠CPD=$\frac{1}{2}$∠COD,因此只需在Rt△OBC中求出∠COB的正弦值即可.
解答 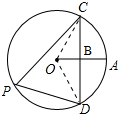 解:连接OC、OD;
解:连接OC、OD;
则∠COB=∠CPD=$\frac{1}{2}$∠COD;
Rt△OBC中,OC=2OB,则BC=$\sqrt{3}$OB;
故tan∠CPD=tan∠COB=$\sqrt{3}$.
故选:D
点评 此题主要考查了圆周角定理、垂径定理以及勾股定理的综合应用.

练习册系列答案
相关题目
19.设等差数列{an}的前n项和为Sn,已知(a7-1)3+2012(a7-1)=1,(a2006-1)3+2012(a2006-1)=-1,则下列结论正确的是( )
| A. | S2012=-2012,a2012>a7 | B. | S2012=2012,a2012>a7 | ||
| C. | S2012=-2012,a2012<a7 | D. | S2012=2012,a2012<a7 |
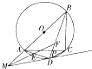 如图,已知四边形ABCD内接于半径为3的圆,且AB是圆的直径.经过点D的圆的切线与BA的延长线交于点M.∠BMD的平分线分别交AD,BD于点E,FAC,BD交于点P.
如图,已知四边形ABCD内接于半径为3的圆,且AB是圆的直径.经过点D的圆的切线与BA的延长线交于点M.∠BMD的平分线分别交AD,BD于点E,FAC,BD交于点P.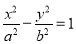 (
(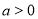 ,
,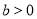 )经过点
)经过点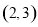 ,且离心率为
,且离心率为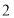 ,则它的焦距为( )
,则它的焦距为( ) B.
B.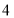
 D.
D.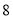
 如图,抛物线C1:x2=2py(p>0)的焦点为F,椭圆C2:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=l (a>b>0)的离心率e=$\frac{\sqrt{3}}{2}$,C1与C2在第一象限的交点为P(2,1).
如图,抛物线C1:x2=2py(p>0)的焦点为F,椭圆C2:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=l (a>b>0)的离心率e=$\frac{\sqrt{3}}{2}$,C1与C2在第一象限的交点为P(2,1).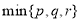 为表示
为表示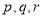 三者中较小的一个, 若函数
三者中较小的一个, 若函数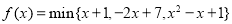 ,则不等式
,则不等式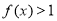 的解集为( )
的解集为( )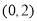 B.
B.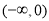
 D.
D.