题目内容
7.若函数f(x),g(x)满足:?x∈(0,+∞),均有f(x)>x,g(x)<x成立,则称“f(x)与g(x)关于y=x分离”.已知函数f(x)=ax与g(x)=logax(a>0,且a≠1)关于y=x分离,则a的取值范围是(${e}^{\frac{1}{e}}$,+∞).分析 由题意可得y=ax与y=logax互为反函数,a>1,故问题等价于ax>x(a>1)在区间(0,+∞)上恒成立,利用导数进行解决.
解答 解:由题意,a>1.
故问题等价于ax>x(a>1)在区间(0,+∞)上恒成立.
构造函数f(x)=ax-x,则f′(x)=axlna-1,
由f′(x)=0,得x=loga(logae),
x>loga(logae)时,f′(x)>0,f(x)递增;
0<x<loga(logae),f′(x)<0,f(x)递减.
则x=loga(logae)时,函数f(x)取到最小值,
故有${a}^{lo{g}_{a}(lo{g}_{a}e)}$-loga(logae)>0,解得a>${e}^{\frac{1}{e}}$.
故答案为:(${e}^{\frac{1}{e}}$,+∞).
点评 本题考查恒成立问题关键是将问题等价转化,从而利用导数求函数的最值求出参数的范围.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
16. 在四棱柱ABCD-A1B1C1D1中,AA1⊥平面A1B1C1D1,底面A1B1C1D1是边长为a的正方形,侧棱AA1的长为b,E为侧棱BB1上的动点(包括端点),则( )
在四棱柱ABCD-A1B1C1D1中,AA1⊥平面A1B1C1D1,底面A1B1C1D1是边长为a的正方形,侧棱AA1的长为b,E为侧棱BB1上的动点(包括端点),则( )
 在四棱柱ABCD-A1B1C1D1中,AA1⊥平面A1B1C1D1,底面A1B1C1D1是边长为a的正方形,侧棱AA1的长为b,E为侧棱BB1上的动点(包括端点),则( )
在四棱柱ABCD-A1B1C1D1中,AA1⊥平面A1B1C1D1,底面A1B1C1D1是边长为a的正方形,侧棱AA1的长为b,E为侧棱BB1上的动点(包括端点),则( )| A. | 对任意的a,b,存在点E,使得B1D⊥EC1 | |
| B. | 当且仅当a=b时,存在点E,使得B1D⊥EC1 | |
| C. | 当且仅当a≤b时,存在点E,使得B1D⊥EC1 | |
| D. | 当且仅当a≥b时,存在点E,使得B1D⊥EC1 |
19.设等差数列{an}的前n项和为Sn,已知(a7-1)3+2012(a7-1)=1,(a2006-1)3+2012(a2006-1)=-1,则下列结论正确的是( )
| A. | S2012=-2012,a2012>a7 | B. | S2012=2012,a2012>a7 | ||
| C. | S2012=-2012,a2012<a7 | D. | S2012=2012,a2012<a7 |
 :若
:若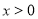 ,则函数
,则函数 的最小值为
的最小值为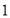 ;命题
;命题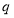 :若
:若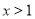 ,则
,则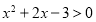 .则
.则 B.
B.
 D.
D.
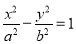 (
(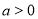 ,
,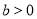 )经过点
)经过点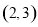 ,且离心率为
,且离心率为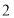 ,则它的焦距为( )
,则它的焦距为( ) B.
B.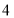
 D.
D.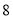
 如图,在三棱锥P-ABC中,△ABC是边长为2的正三角形,∠PCA=90°,E,H分别为AP,AC的中点,AP=4,BE=$\sqrt{3}$.
如图,在三棱锥P-ABC中,△ABC是边长为2的正三角形,∠PCA=90°,E,H分别为AP,AC的中点,AP=4,BE=$\sqrt{3}$.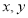 满足条件
满足条件 ,且
,且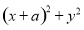 的最小值为6,
的最小值为6,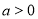 ,则
,则 _____________.
_____________.