题目内容
13.已知函数f(x)=x2-ax+1,其中a∈R,且a≠0.(1)若f(x)在[-1,1]上不是单调函数,求a的取值范围;
(2)求y=|f(x)|在区间[0,|a|]上的最大值.
分析 (1)由题意可得,-1<$\frac{a}{2}$<1,由此求得a的范围.
(2)由条件利用二次函数的性质,分类讨论求得y=|f(x)|在区间[0,|a|]上的最大值.
解答 解:(1)∵函数f(x)=x2-ax+1在[-1,1]上不是单调函数,∴-1<$\frac{a}{2}$<1,∴-2<a<2.
(2)①当a<0时,y=|f(x)|在区间[0,|a|]上递增,∴y=|f(x)|的最大值为2a2+1.
②当a>0时,f(0)=f(|a|)=1,f($\frac{a}{2}$)=1-$\frac{{a}^{2}}{4}$,
当0<a≤2$\sqrt{2}$ 时,y=|f(x)|的最大值为1.
当a>2$\sqrt{2}$时,y=|f(x)|的最大值为$\frac{{a}^{2}}{4}$-1.
∴综上,|f(x)|max=$\left\{\begin{array}{l}{{2a}^{2}+1,a<0}\\{1,0<a≤2\sqrt{2}}\\{\frac{{a}^{2}}{4}-1,a>2\sqrt{2}}\end{array}\right.$.
点评 本题主要考查求二次函数在闭区间上的最值,二次函数的性质的应用,体现了分类讨论的数学思想,属中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
18.已知中心在坐标原点的椭圆与双曲线有公共焦点,且左、右焦点分别为F1、F2,这两条曲线在第一象限的交点为P,△PF1F2是以PF1为底边的等腰三角形,若|PF1|=10,设椭圆与双曲线的离心率分别为e1,e2,则e1+e2的取值范围是( )
| A. | ($\frac{5}{4}$,+∞) | B. | ($\frac{4}{3}$,+∞) | C. | ($\frac{3}{2}$,+∞) | D. | ($\frac{5}{3}$,+∞) |
3.某市对汽车限购政策进行了调查,在参加调查的300名有车人中116名持反对意见,200名无车人中有121名持反对意见,在运用这些数据说明“拥有车辆”与“反对汽车限购政策”是否有关系时,最有说服力的方法是( )
| A. | 平均数与方差 | B. | 回归直线方程 | C. | 独立性检验 | D. | 概率 |
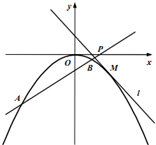 已知曲线C:x2=-2py(p>0),点M是曲线C上的一个动点,过点M且与曲线C相切的直线l的方程为x+y-1=0.
已知曲线C:x2=-2py(p>0),点M是曲线C上的一个动点,过点M且与曲线C相切的直线l的方程为x+y-1=0. 已知函数y=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)在一个周期内的图象如图所示,M、N分别是这段图象的最高点和最低点,且$\overrightarrow{OM}•\overrightarrow{ON}$=0(O为坐标原点),则A=$\frac{\sqrt{7}}{12}$π.
已知函数y=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)在一个周期内的图象如图所示,M、N分别是这段图象的最高点和最低点,且$\overrightarrow{OM}•\overrightarrow{ON}$=0(O为坐标原点),则A=$\frac{\sqrt{7}}{12}$π.