题目内容
3.已知函数f(x)=$\frac{1}{2}$x2sinx+xcosx,则其导函数f′(x)的图象大致是( )| A. | 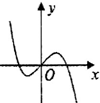 | B. | 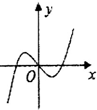 | C. | 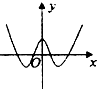 | D. |  |
分析 先求导,再根据函数的奇偶性排除A,C,再根据函数值得变化趋势得到答案.
解答 解:∵f(x)=$\frac{1}{2}$x2sinx+xcosx,
∴f′(x)=$\frac{1}{2}$x2cosx+cosx,
∴f′(-x)=$\frac{1}{2}$(-x)2cos(-x)+cos(-x)=$\frac{1}{2}$x2cosx+cosx=f′(x),
∴其导函数f′(x)为偶函数,图象关于y轴对称,故排除A,B,
当x→+∞时,f′(x)→+∞,故排除D,
故选:C.
点评 本题考查了导数的运算法则和函数图象的识别,属于中档题.

练习册系列答案
 小学生10分钟口算测试100分系列答案
小学生10分钟口算测试100分系列答案
相关题目
13. 设f(x)是一个三次函数,f′(x)为其导函数,如图是函数y=x•f′(x)的图象的一部分,则函数f(x)的极大值是( )
设f(x)是一个三次函数,f′(x)为其导函数,如图是函数y=x•f′(x)的图象的一部分,则函数f(x)的极大值是( )
 设f(x)是一个三次函数,f′(x)为其导函数,如图是函数y=x•f′(x)的图象的一部分,则函数f(x)的极大值是( )
设f(x)是一个三次函数,f′(x)为其导函数,如图是函数y=x•f′(x)的图象的一部分,则函数f(x)的极大值是( )| A. | f(-1) | B. | f(-2) | C. | f(1) | D. | f(2) |
18.已知中心在坐标原点的椭圆与双曲线有公共焦点,且左、右焦点分别为F1、F2,这两条曲线在第一象限的交点为P,△PF1F2是以PF1为底边的等腰三角形,若|PF1|=10,设椭圆与双曲线的离心率分别为e1,e2,则e1+e2的取值范围是( )
| A. | ($\frac{5}{4}$,+∞) | B. | ($\frac{4}{3}$,+∞) | C. | ($\frac{3}{2}$,+∞) | D. | ($\frac{5}{3}$,+∞) |
12.若复数z满足(3-4i)z=|4+3i|,则z的虚部为( )
| A. | $\frac{4}{5}$ | B. | -$\frac{4}{5}$i | C. | $\frac{4}{5}$i | D. | 4 |
13.已知函数f(x)是定义在R上的偶函数,且在区间[0,+∞)上是减函数,若$f({ln\frac{n}{m}})-f(1)>0$,则$\frac{{{m^2}+{n^2}}}{mn}$的取值范围是( )
| A. | [2,+∞) | B. | [2,e) | C. | $({e+\frac{1}{e},+∞})$ | D. | $[{2,e+\frac{1}{e}})$ |
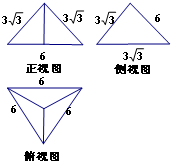 正四面体(即各条棱长均相等的三棱锥)的棱长为6,某学生画出该正四面体的三视图如下,其中有一个视图是错误的,则该视图修改正确后对应图形的面积为6$\sqrt{6}$.该正四面体的体积为18$\sqrt{2}$.
正四面体(即各条棱长均相等的三棱锥)的棱长为6,某学生画出该正四面体的三视图如下,其中有一个视图是错误的,则该视图修改正确后对应图形的面积为6$\sqrt{6}$.该正四面体的体积为18$\sqrt{2}$.