题目内容
8. 如图,在四棱锥P-ABCD中,AB∥CD,PA⊥AD,CD⊥AD,PA=AD=CD=2AB,E,F分别为PC,CD的中点,DE=EC.
如图,在四棱锥P-ABCD中,AB∥CD,PA⊥AD,CD⊥AD,PA=AD=CD=2AB,E,F分别为PC,CD的中点,DE=EC.(Ⅰ)求证:平面ABE⊥平面BEF;
(Ⅱ)求锐二面角E-BD-C的余弦值.
分析 (Ⅰ)由题目给出的条件,可得四边形ABFD为矩形,说明AB⊥BF,再证明AB⊥EF,由线面垂直的判定可得AB⊥面BEF,再根据面面垂直的判定得到平面ABE⊥平面BEF;
(Ⅱ)以A点为坐标原点,AB、AD、AP所在直线分别为x、y、z轴建立空间坐标系,求出平面法向量,利用向量的夹角公式求出二面角的余弦值.
解答 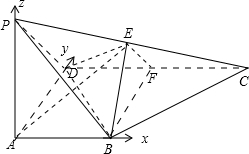 证明:(Ⅰ)如图,
证明:(Ⅰ)如图,
∵AB∥CD,CD⊥AD,AD=CD=2AB=2,F为CD的中点,
∴ABFD为矩形,AB⊥BF.
∵DE=EC,∴DC⊥EF,又AB∥CD,∴AB⊥EF
∵BF∩EF=F,∴AB⊥面BEF,又AB?面ABE,
∴平面ABE⊥平面BEF.
(2)解:∵DE=EC,∴DC⊥EF,
又PD∥EF,AB∥CD,∴AB⊥PD
又AB⊥PD,∴AB⊥面PAD,AB⊥PA.
以AB所在直线为x轴,AD所在直线为y轴,AP所在直线为z轴建立空间坐标系,
则B(1,0,0),D(0,2,0),P(0,0,2),C(2,2,0),E(1,1,1)
平面BCD的法向量$\overrightarrow{{n}_{1}}$=(0,0,1),
设平面EBD的法向量为$\overrightarrow{{n}_{2}}$=(x,y,z),
∵$\overrightarrow{BD}$=(-1,2,0),$\overrightarrow{BE}$=(0,1,1),
∴$\left\{\begin{array}{l}{-x+2y=0}\\{y+z=0}\end{array}\right.$,
∴$\overrightarrow{{n}_{2}}$=(2,1,-1),
∴cos<$\overrightarrow{{n}_{1}}$,$\overrightarrow{{n}_{2}}$>=$\frac{\sqrt{6}}{6}$.
点评 本题考查了面面垂直的判定,考查了利用空间向量求二面角的大小,解答的关键是建立正确的空间坐标系,该题训练了学生的计算能力,是中档题.

 小学生10分钟口算测试100分系列答案
小学生10分钟口算测试100分系列答案| A. | ($\frac{5}{4}$,+∞) | B. | ($\frac{4}{3}$,+∞) | C. | ($\frac{3}{2}$,+∞) | D. | ($\frac{5}{3}$,+∞) |
| A. | 平均数与方差 | B. | 回归直线方程 | C. | 独立性检验 | D. | 概率 |
| A. | [2,+∞) | B. | [2,e) | C. | $({e+\frac{1}{e},+∞})$ | D. | $[{2,e+\frac{1}{e}})$ |
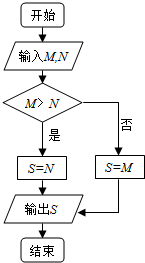
| A. | 1 | B. | ln2 | C. | $\frac{π}{2}$ | D. | 0 |
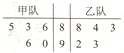 某项比赛规则是:先进行个人赛,每支参赛队的成绩前三名队员再代表本队进行团体赛,团体赛是在两队名次相同队员之间进行且三场比赛同时进行.根据以往比赛统计:两名队员中个人赛成绩高的队员在各场获胜的概率为$\frac{2}{3}$,负的概率为$\frac{1}{3}$,且各场比赛互不影响.已知甲乙队各5名队员,这10名队员的个人赛成绩如图所示:
某项比赛规则是:先进行个人赛,每支参赛队的成绩前三名队员再代表本队进行团体赛,团体赛是在两队名次相同队员之间进行且三场比赛同时进行.根据以往比赛统计:两名队员中个人赛成绩高的队员在各场获胜的概率为$\frac{2}{3}$,负的概率为$\frac{1}{3}$,且各场比赛互不影响.已知甲乙队各5名队员,这10名队员的个人赛成绩如图所示: